Lineare Gleichungssysteme mit 3 Unbekannten
Ein lineares Gleichungssystem ist nur dann eindeutig lösbar, wenn es aus mindestens so vielen Gleichungen besteht wie Variablen darin enthalten sind. Aber auch in diesem Fall ist die eindeutige Lösbarkeit nicht immer gegeben.
Wenn ein Dreieckssystem allerdings in Dreiecksgestalt gegeben ist, dann lässt es sich schrittweise durch Einsetzen lösen.
Wir wollen gemeinsam das Gleichungssystem mit drei Unbekannten lösen. Gegeben haben wir das folgende Gleichungssystem:
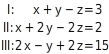
- Jetzt erzeugen wir das Dreiecksform
In den Gleichungen I und II ist der Koeffizient von x jeweils 1. Eine Gleichung ohne x ergibt sich, indem du Gleichung I mit -1 multiplizierst und das Ergebnis zu Gleichung II addierst.
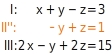
Die ersten beiden Gleichungen passen schon in die Dreiecksgestalt.
Du erstellst aus Gleichung I und III eine weitere Gleichung ohne die Variable x , indem du Gleichung I mit -2 multiplizierst und das Ergebnis zu Gleichung III addierst. Gleichung III wird durch die neue Gleichung
III’ (= III + (-2)I) ersetzt
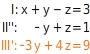
Die Gleichungen II” und III’ enthalten nur noch zwei Variablen. Du multiplizierst Gleichung II” mit (-3) und addierst die Gleichung zu III’. Du erhältst Gleichung III” (=III’+(-3)II”), die nur noch die Variable z enthält.
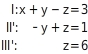
Das Gleichungssystem ist in Dreiecksgestalt:
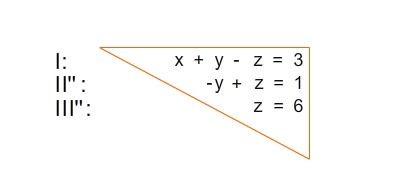
Du löst das Gleichungssystem bei Gleichung III” beginnend schrittweise durch Einsetzen und Umstellen und berechnest die Lösung.
unsere Lösung lautet somit L = { 4 ; 5 ; 6 }
Merke Dir
Jede Lösung eines Gleichungssystems aus drei Gleichungen mit drei Variablen ist ein Zahlentripel. Beim Lösen von linearen Gleichungssystemen mit mehr als zwei Gleichungen und Variablen geht man systematisch vor.
Äquivalente Umformungen sind u. a.:
- Gleichungen vertauschen
- Beide Seiten einer Gleichung mit derselben von 0 verschiedenen Zahl multiplizieren
- Beide Seiten einer Gleichung durch dieselbe von 0 verschiedene Zahl dividieren
- Eine Gleichung zu einer anderen Gleichung addieren
- Eine Gleichung von einer anderen Gleichung subtrahieren
Nach diesem Schema könnt Ihr weitere Gleichungssysteme mit 3 Unbekannten lösen.
