Analytische Geometrie

Analytische Geometrie: Anwendungen

Das Fachgebiet kommt in den Naturwissenschaften zur Anwendung. Besonders häufig ist es in der Physik anzutreffen. Ein typisches Beispiel ist die Berechnung von Planetenbahnen. Früher befasste sie sich mit Fragestellungen der räumlichen (euklidischen) und ebenen Geometrie. Die allgemeine Definition lautet: Beschreibung affiner Räume beliebiger Dimensionen über beliebigen Körpern. In Chemie und Technik ist sie ebenfalls ein unverzichtbares Mittel. In den Fachhochschulen und Universitäten ist sie Teil des Lehrplans technischer und naturwissenschaftlicher Studiengänge.

Sie ist der Grundstein der Computergrafik und in der elektronischen Verarbeitung grafischer Daten von enormer Wichtigkeit. Deshalb ist sie in der Informatik ein im Detail behandeltes Gebiet. Die Grundlage entsteht in der Grundschule. Dort kommt das Thema mit vereinfachten Aufgabenstellungen zum Zug. Typische Aufgaben drehen sich um:

• Drei- und Vierecke im Raum,
• Höhe eines schiefen Prismas,
• Lage von Geraden im Raum,
• lineare Abhängigkeit von Vektoren,
• Ebenen-Gleichungen.

Mithilfe des Fachgebiets gelingt es, räumliche Probleme in eine mathematische Form zu bringen und zu berechnen.

Geschichtlicher Abriss

Die ersten Berechnungen in der Geometrie gehen auf das Altertum zurück. Die Strahlensätze, der Satz des Pythagoras und das Gebiet der Trigonometrie gehören zu den ersten Errungenschaften der frühen analytischen Geometrie. Die Mathematiker Pierre de Fermat und René Descartes entdeckten Anfang des 17. Jahrhunderts eine neuartige Methode zur Berechnung geometrischer Probleme. Fermat sucht die Kurve zu einer gegebenen Koordinatengleichung, Descartes die Koordinaten zu einer bestehenden Kurve. Die analytische Geometrie nahm mit diesen zwei großen Persönlichkeiten ihren Anfang.

Descartes gilt als Vater des Gebiets. Er löste sich von der konstruktiven synthetischen Geometrie der Griechen und algebraisierte die Probleme rund um Figuren und Körper. Dazu führte er das Koordinatensystem ein: den Ursprung (Bezugspunkt 0) mit zwei Koordinatenachsen. Damit ordnete er jedem Punkt der Ebene zwei Koordinaten zu. Dies ermöglichte die Darstellung geometrischer Figuren wie Kreise oder Geraden als Lösungsmengen von Gleichungen. Ihre Schnittpunkte berechnete er mithilfe von Gleichungssystemen. Die Darstellung von Körpern und Figuren in Ebene und im Raum sind Teil des Fachgebiets.

Heute versteht sich der Begriff anders. Analytische Geometrie ist die Verwendung der Koordinatenrechnung in der Geometrie. Die algebraische Geometrie ist eine Weiterentwicklung. Sie behandelt Gleichungen höheren Grades. Die Differenzialgeometrie ist ebenfalls eine Folge der analytischen Geometrie. Zu ihr gehört beispielsweise die Analysis. Sie wagt sich in Räume höherer Dimensionen vor. Alle Teilgebiete sind wichtige Integranden technischer und naturwissenschaftlicher Studiengänge.

Koordinaten und Vektoren

Die analytische Geometrie beruht auf Koordinaten und Vektoren. Das Koordinatensystem ist ihr entscheidendes Hilfsmittel. Meistens kommt in der Praxis die kartesische Ausführung zum Zug. Es dient zur Berechnung von Abständen und Winkeln. Für die Kalkulation von Teilverhältnissen oder um Gerade auf Parallelität zu untersuchen genügt ein schiefwinkliges Koordinatensystem.

Ein Vektor ist ein Pfeil. Seine Darstellung beinhaltet Richtung, Betrag und Angriffspunkt. Mit seiner Hilfe sind Darstellungen in der analytischen Geometrie besser zu verstehen. Die Vektorrechnung vereinfacht und vereinheitlicht Rechnungen des Fachgebiets. Die Vektoren waren nicht Bestandteil der Erfindung der analytischen Geometrie. Sie sind ohne geometrischen Bezug definierbar. Dennoch ist ihre Verwendung im kartesischen Koordinatensystem heute gebräuchlich. In der Sekundarstufe II und im mathematisch-physikalisch-technischen Grundstudium sind lineare Algebra und analytische Geometrie Gegenstand ein und desselben Kurses.

Gleichungen

Zur Beschreibung von geometrischen Objekten wie Kreisen, Kugeln, Ebenen und Geraden kommen verschiedene Arten von Gleichungen zum Einsatz. Die implizite und explizite Koordinatengleichung basiert auf den Koordinaten x und y. Die Parametergleichung benutzt Vektoren, um Gebilde zu beschreiben. Alle drei Formen sind Teil der analytischen Geometrie. Je nach Aufgabe kommt eine der beschriebenen Gleichungen zum Einsatz.

Analytische Geometrie in Ebene und Raum

Eine Ebene ist durch die x- und die y-Koordinate beschrieben. Ein beliebiger Punkt der Ebene ist durch zwei Koordinaten definiert. Die Gerade in der Ebene ist durch die implizite Koordinatengleichung

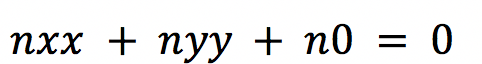
definiert. Eine andere Form ist die Parametergleichung. Punkte im Raum sind über drei Koordinaten definiert. Damit ist jeder Punkt im definierten Raum beschreibbar. Ebenen und Körper erhalten durch eine Formel rechnerischen Charakter. Die analytische Geometrie zeigt sich in der Berechnung von Körpern und Figuren in Ebene und Raum.

Vektoren und ihre Eigenschaften

Obwohl Vektoren ursprünglich nicht Teil der analytischen Geometrie waren, gehören sie heute dazu. Ein Vektor ist zu seinesgleichen addierbar und mit Zahlen multiplizierbar. Er ist ein mathematisches Objekt, das eine Parallelbeschreibung im Raum oder der Ebene beschreibt. Diverse Begriffe sind bei Vektoren wichtig, da sie in der analytischen Geometrie zur Anwendung kommen. Das Skalarprodukt ist die Multiplikation zweier Vektoren unter Einbezug des von ihnen eingeschlossenen Winkels. Das Spatprodukt ist das Produkt dreier Vektoren. Es ist ein gemischtes Produkt. Die analytische Geometrie arbeitet in der heutigen Zeit mit Vektoren. Sie sind ein fester Bestandteil des Fachgebiets.

Herausforderungen

Die analytische Geometrie verfügt über eine einfach zu verstehende Basis. Kompliziert sind die unzähligen Formeln und Rechenarten. Wer beim Lernen langsam Schritt für Schritt vorwärtsgeht, hat bessere Chancen, den Überblick zu behalten. Wer die Basis versteht, ist in der Lage, immer neue Formeln zu lernen und in das bestehende System zu integrieren. Obwohl es sich um Berechnungen geometrischer Körper und Figuren handelt, ist die visuelle Darstellung steht Teil der Aufgabe. Sie hilft, den Sachverhalt besser zu verstehen und sich im räumlichen Darstellungsvermögen zu üben.

Die analytische Geometrie ist ein Gebiet der Sekundarstufe II. Sie hat ihren Ursprung in geometrischen Grundbegriffen, die in der Grundschule Bestandteil des Lehrplans sind. Schwierigkeiten im Fach gründen oftmals darauf, dass der Lernende Defizite in den Grundbegriffen mit sich bringt. Eine Wiederholung geometrischer Themen ist keine verlorene Zeit, sondern die Stärkung der Basis zum Aufbau eines weitergehenden geometrischen Verständnisses.