Differentialrechnung

Geschichte der Differenzialrechnung – die Entstehung

Im 17. Jahrhundert erschien das Tangentenproblem als Vorläufer der Differenzialrechnung. Es zeigte sich als naheliegenden Lösungsansatz, eine Tangente an eine Kurve durch ihre Sekante über ein endliches, beliebig kleines Intervall anzunähern. Es war eine Herausforderung mit infinitesimal geringen Intervallbreiten zu rechnen. Einer der ersten, die sich an das Problem heranwagten, war Pierre de Fermat. 1628 entwickelte er eine Methode, um Extremstellen von algebraischen Termen zu bestimmen und Tangenten an Kurven wie beispielsweise Kegelschnitten zu berechnen.

Grenzübergänge und Ableitungen waren zu dieser Zeit nicht Teil davon. Fermats Entdeckung inspirierte Leibniz und Newton, widerspruchsfrei funktionierende Kalküle zu entwickeln. Die beiden Begründer der Differenzialrechnung entwickelten ihre Berechnungen unabhängig voneinander. Isaac Newtons Ausgangspunkt war das physikalische Momentan-Geschwindigkeits-Problem. Gottfried Wilhelm Leibniz löste das Problem geometrisch über die Tangente. Die heutigen Ableitungsregeln basieren auf den Werken von Leonhard Euler.

Die heute übliche logische Strenge erhielt das Gebiet Anfang des 19. Jahrhunderts durch Augustin-Louis Cauchy. Er ging von der infinitesimalen Größe ab und definierte die Ableitung als Grenzwert von Sekantensteigungen. Karl Weierstraß beschrieb Ende des 19. Jahrhunderts die heute gültige Definition des Grenzwertes, der an Gymnasien und Hochschulen Gegenstand des Unterrichts ist.

Tangentenproblem

Das Tangentenproblem ist die Basis der Differenzialrechnung. Die Steigung einer Tangente an einer Kurve zu berechnen, bringt das Problem mit sich, dass nur ein Punkt (Schnittpunkt) zur Verfügung steht. Als Hilfsmittel ist zuerst die Berechnung der Steigung einer Sekante angebracht, wovon einer ihrer Punkte auf dem Kreis mit demjenigen der Tangente identisch ist. Die Sekantensteigung ist die Differenz zweier Quotienten, auch Differenzenquotient genannt. Als abgekürzte Formel ergibt er:

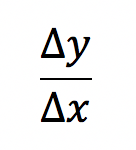
Ein Beispiel aus dem täglichen Leben für einen Differenzenquotienten ist die Durchschnittsgeschwindigkeit eines Autos.

Um seine Momentangeschwindigkeit zu berechnen, ist die Annäherung der beiden Sekantenpunkte gefragt. Dabei gehen und  gegen Null. In vielen Fällen bleibt der Wert des Bruches endlich. Daraus leitet sich die Differenzierbarkeit einer Funktion ab. Eine Funktion mit einem offenen Intervall in den reellen Zahlen ist differenzierbar, falls der Grenzwert Limes existiert. Das bedeutet: Eine differenzierbare Funktion besitzt eine eindeutige Tangente in jedem Punkt des Graphen innerhalb des Definitionsbereichs.

Ableitung

Als Klärung des Grundbegriffes der Differenzialrechnung folgt die arithmetische sowie die geometrische Definition der Ableitung. Geometrisch ausgedrückt ist die Ableitung eine verallgemeinerte Steigung. Ursprünglich ist sie nur für lineare Funktionen mit einer Geraden als Funktionsgraph definiert. An einer beliebigen Stelle x0 ist sie als Steigung der Tangente im Punkt (x0; f (x0)) bestimmt. Arithmetisch gesehen ist die Ableitung einer Funktion f für jedes x die Größe des linearen Anteils der Änderung von . Dazu ändert sich x um einen beliebig kleinen Betrag . Der Grenzwert, Limes genannt, dient der exakten Formulierung dieses Sachverhaltes der Differenzialrechnung. Der Mathematiker Leibniz beschreibt die Ableitung folgendermaßen: der Proportionalitätsfaktor zwischen infinitesimalen Änderungen des Eingabewertes und infinitesimalen Änderungen des daraus resultierenden Funktionswertes. Existiert für eine Funktion dieser Faktor ist sie differenzierbar. Die Ableitung in einem Punkt ist die Steigung derjenigen linearen Funktion, welche die Änderungen der gegebenen Funktion an diesem Punkt am besten approximiert. Deshalb heißt die Ableitung auch Linearisierung der Funktion. Sie berechnet sich aus dem Differenzenquotienten der Sekante der Funktion.

Ableitungsregeln

Für die Ableitung zusammengesetzter Funktionen stehen Ableitungsregeln bereit, welche sie auf Ableitungen einfacherer Funktionen zurückführt. Folgende Ableitungsregeln helfen beim Herleiten:

• Faktorregel,
• Produktregel,
• Potenzregel,
• Summenregel,
• Quotientenregel,
• Kettenregel.

Die Potenzregel dient zum Finden der Ableitungen von Funktionen der Formel:

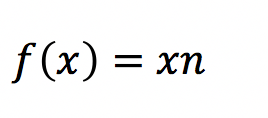
Ein unabhängiger Faktor vor der Potenz übernimmt der Ausführende laut der Faktorregel. Sie dient zur Ableitung von Funktionen der allgemeinen Formel:

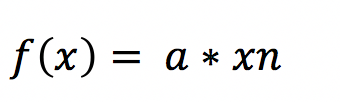
Bei einer Funktion aus mehreren Termen sind diese als einzelne Funktionen zu betrachten und nach der Summenregel mit der Formel:

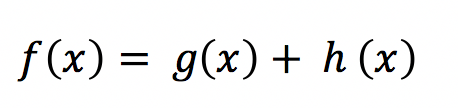
abzuleiten. Dasselbe gilt für eine Funktion aus mehreren Faktoren. Jeder ist für sich als einzelne Funktion zu sehen:

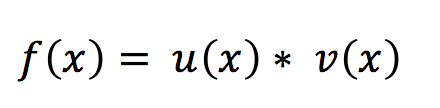
Diese Ableitungen sind in der Produktregel definiert.

In der Differenzialrechnung spielt die Quotientenregel eine wichtige Rolle. Ist die vorliegende Funktion ein Bruch, sind Nenner und Zähler als einzelne Funktionen zu betrachten:

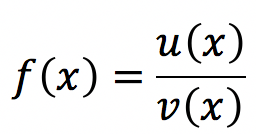
Die Kettenregel

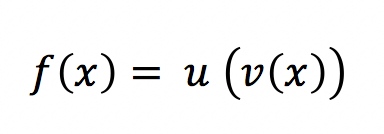
dient zur Untersuchung von mehreren ineinander verschachtelten Funktionen. In der tabellarischen Übersicht sind die Ableitungen von trigonometrischen Funktionen, Logarithmus und Exponentialfunktionen aufgeführt.

Wendepunkt und Sattelpunkt

In einem Wendepunkt ändert die Funktion ihre Richtung. Graphisch gesehen ist er leicht zu erkennen. Mathematisch ausgedrückt ist er dort, wo die Ableitungsfunktion einen Extrempunkt hat und die Steigung am stärksten ist. Er ist durch die Ableitung der Ableitung, zweite Ableitung genannt, zu berechnen. Der Sattelpunkt ist eine Sonderform des Wendepunktes. In ihm verläuft der Graph parallel zur x-Achse.

Schwierigkeiten und Herausforderungen

Die Differenzialrechnung baut auf dem Grundbegriff der Funktion auf. Es geht um Berechnung und grafische Darstellung sowie ihre Ableitungen. Das Thema beginnt in der Sekundarstufe I mit einfachen Begriffen. An der Universität und Fachhochschulen findet das Fachgebiet Eingang in technische und naturwissenschaftliche Berufe. Für die Mathematik ist es grundlegend und bietet Basis für viele Berechnungen. Schwierigkeiten im Verständnis entstehen dadurch, dass die Basics nicht genügend gefestigt sind. Wer die Grundbegriffe versteht und durchschaut, ist gut in der Lage, die Differenzialrechnung darauf aufzubauen.