Darstellung von Mengen
In der Mengenlehre werden die Mengen in Diagrammen dargestellt, welche zumeist ein Kreis oder eine Ellipse sind. Diese Darstellung hat sich nicht nur als praktisch herausgestellt, sondern sich auch durchgesetzt. So dass man nun das eine mit dem anderen verbindet und die Aussage schnell versteht.
Was man darstellt ist abhängig vom Zweck der Darstellung. Dass heißt, man kann die Menge so einteilen und beschreiben, dass sie der Aufgabe oder der Absicht entspricht. Dies kann eine Menge aus dem Alltag sein, aber auch eine Menge aus der Mathematik.
Beispiel 1
Wir möchten eine Menge darstellen, die Desserts beinhaltet. Dies machen wir mit einem Mengenkreis: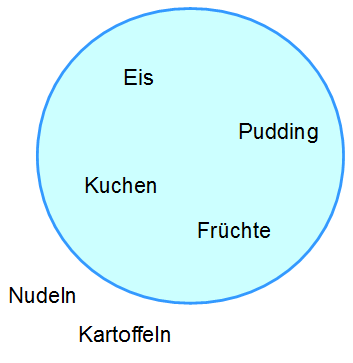
Wir stellen die gewünschte Menge in einem Kreis dar. Der Kreis beinhaltet einige Beispiele für Lebensmittel, die wir als Dessert kennen. Außerhalb des Kreises finden wir zwar auch Lebensmittel. Diese sind allerdings keine Desserts, daher sind sie nicht im Kreis.
Wenn wir kein Diagramm zeichnen wollen, sondern es notieren, geht dies auf folgende Weise:
D = { Eis, Kuchen, Pudding, Früchte}, damit beschreiben wir, dass in unserer Menge Dessert D sich die Eis, Kuchen etc befinden. Um einzelne Element zu definieren, ob sie in der definierten Menge sind, können wir dieses mit dem Elementsymbol ∈ machen.
Somit schreiben wir Kuchen ∈ D, wir sprechen: Kuchen ist Element von D,
aber Nudeln ∉ D, wir sprechen: Nudeln sind nicht Element von D.
Hier haben wir das Beispiel für eine Menge mit Dessert gewählt. Der Inhalt einer Menge kann jedoch alles enthalten. Im Folgenden werden wir Buchstaben, Zahlen und weiteren mathematischen Begriffen nutzen.
Unser Lernvideo zu : Darstellung von Mengen
Mächtigkeit von Menge
Abgesehen davon wie wir Mengen darstellen, ist es auch wichtig Mengen zu vergleichen. Beim Vergleich von Mengen beachten wir, wie viele Elemente in den einzelnen Mengen sind. dieses nennt man die Mächtigkeit von Elementen. Die Mächtigkeit weißt nur auf die Differenz zweier Mengen hin, aber nicht, dass sie allgemein groß sind.
Die Mächtigkeit einer Menge beinhaltet die Anzahl der Elemente.
Wollen wir nun zwei Mengen miteinander auf ihre Mächtigkeit vergleichen, zählen wir die einzelnen Elemente. Wir betrachten zwei verschiedene Mengen A und B.
Menge A = {z, y, x, w}
Menge B = {9, 8, 7, 6, 5, 4}
Wir zählen beide Mengenelemente und erfahren dadurch, dass Menge A 4 Elemente und Menge B 6 Elemente hat. Dieses notieren wir mit Betragstrichen für A und B:
|A| = 4 und |B| = 6
Das bedeutet, dass die beiden Mengen eine differenzierte Mächtigkeit haben und somit nicht gleich groß sind, sondern Menge B größer als Menge A ist.
Gleichheit von Mengen
Nun können wir die Mächtigkeit, also die Größe, von Mengen erfahren und bestimmen, ob verschiedene Mengen gleich groß sind oder auch unterschiedlich mächtig.
Nun gibt es noch den Begriff der Gleichheit von Mengen. Die Gleichheit ist nicht nur bedeutend damit, dass die Mengen die selbe Mächtigkeit haben, sondern auch die selben Elemente beinhalten. Erst wenn beides zutrifft sprechen wir von Gleichheit von zwei Mengen.
Zwei Mengen sind gleich, wenn in beiden Mengen die selbe Anzahl als auch die selben Elemente vorhanden sind.
Beispiel:
Haben wir nun die Menge A = {z, y, x, w, v} und die Menge B = {x, y, w, v, z}.
Wenn wir diese beiden Mengen vergleichen, zählen wir zunächst die Elemente. In beiden sind 5 Elemente, dadurch sind sie schon mal gleich mächtig. Als nächstes sortieren wir die Elemente auf die selbe Art und Weise. So haben wir Menge A = {z, y, x, w, v} und Menge B = {z, y, x, w, v}. Nun sehen wir, dass die selben Elemente in Menge A als auch in Menge B sind. Die Mengen sind also gleich.
Sollte bei anderen Mengen nur ein Element anders sein, haben wir keine Gleichheit der Mengen.
