Modellieren mit linearen Gleichungssystemen
Unter Modellieren versteht man in der Mathematik das Umsetzen einer realen Situation in eine mathematische Formel und dann die Anwendung auf die Anfangssituation.
Dieses ist ein Kreislauf und man nennt es mathematisches Modellieren. Bereits in einem vorherigen Thema haben wir dieses angesprochen. Gerne könnt ihr jeder Zeit auf dieser Homepage nachlesen, welche Bedeutung es hat.
Zur Erinnerung
Wir erklären nochmal kurz, was mathematisches Modellieren bedeutet an einer bildlichen Darstellung.
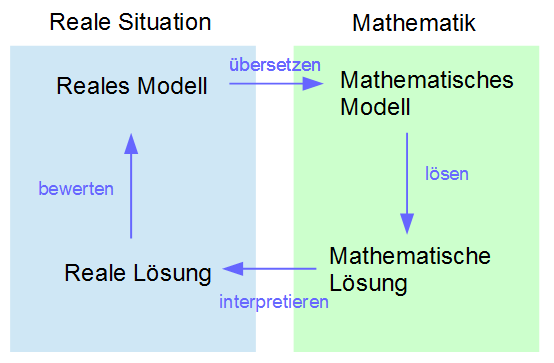
Bei jeder mathematischen Modellierung wird zunächst eine reale Situation geschildert und eine bestimmte Frage dazu gestellt. Danach wird es in eine mathematische Aufgabe übersetzt, diese wird dann gelöst. Daraufhin wird das Ergebnis der mathematischen Aufgabe auf die reale Situation interpretiert und als letztes bewertet. Das Modellieren ist ein Kreislauf, der in jeder Altersstufe genutzt wird. Es ist ein Teil der angewandten Mathematik und kann vielen Schülern beim Verstehen unterstützen, besonders wenn es zuvor sehr mathematisch war, hilft der reale Bezug.
Anwendung bei Gleichungssystemen
Nun möchten wir euch zeigen, wie in diesem Thema der Gleichungssysteme das mathematische Modellieren angewendet werden kann.
Mithilfe von linearen Gleichungssystemen können Preise oder Angebote verglichen werden. Dies hilft besonders bei der Entscheidungsfindung beim Kauf oder Mietung von Gegenständen, Buchung von Urlauben oder ähnliches. In der Schule werden euch des öfteren Sachaufgaben bzw. Textaufgaben gegeben, die ihr lösen sollt. Hier schauen wir uns ein Beispiel an, dass euch verdeutlichen soll, wie ihr an solche Aufgaben herangehen könnt.
Zunächst erfolgt eine Aufgabenstellung wie diese hier:
Michaels Vater benötigt einen neuen Drucker. Dazu schaut er sich verschiedene Angebote im Fachgeschäft an. Er findet zwei Angebote sehr attraktiv, möchte aber gerne wissen, welches mehr lohnen wird.
1. Angebot: Tintenstrahldurcker RT3000, Preis: 150€, Druckpatrone: 80€ für 500 Drucke
2. Angebot: Laserdrucker V543, Preis: 230€, Druckpatrone: 100€ für 2000 Drucke1.
Nun nutzen wir das mathematische Modellieren zur Lösung der Aufgae:
1. Schritt: Übersetzen der Realen Situation ins mathematische Modell.
Beide Angebote lassen sich durch eine lineare Funktion darstellen. Dabei steht x für die verbrauchten Ausdrucke, die Zahl vor x für die Kosten eines Ausdrucks und y für die allgemeinen Kosten in Euro. Die Einkaufkosten sind eine Konstante und werden addiert. Somit können wir folgende Funktionen aufstellen:
1. Angebot: y = 0,16x + 150
2. Angebot: y = 0,05x + 230
2. Schritt: Lösen des mathematischen Modells.
In diesem Fall interessiert uns der Schnittpunkt der beiden linearen Funktionen. Dieses lösen wir mit einem der verschieden Verfahren. Gerne könnt ihr diese nochmals nachlesen um sie euch nochmal zu vergegenwärtigen. Welches Verfaren am besten geeignet ist, erkennt ihr an den Aufgaben. In diesem Fall bietet sich das Gleichsetzungsverfahren an, da beide Gleichungen bereits nach y aufgelöst sind. Somit haben wir folgende Aufgabe zu lösen:
Gleichsetzen:
0,16x + 150 = 0,05x + 230 | -150
0,16x = 0,05x + 80 | -0,05x
0,11x = 80 | :0,11
x = 727,27
Einsetzen:
y = 0,16 • 727,27 + 150
y = 266,36
Schnittpunkt: (727,27/266,36)
3. Schritt: Interpretieren des mathematischen Ergebnisses in die reale Situation.
Wir haben einen Schnittpunkt errechnet. Dieser bedeutet, dass nach 727,27 Ausdrucken die Kosten für die Drucker gleich sind. Zuvor ist Angebot 1 günstiger, danach rechnet sich Angebot 2.
4. Schritt: Bewerten des realen Ergebnisses
Nun können wir die Fagestellung vom Anfang beantworten. Um die Frage des Vaters zu beantworten, kannst man ihm mitteilen, dass bis zum 727. Ausdruck sich das 1. Angebot lohnt und danach das 2. Angebot.
Dieses ist ein Beispiel zur Nutzung des mathematischen Modellierens. Dabei ist es immer wichtig, herauszufinden, auf was abgezielt wird und was dabei wichtig und weniger wichtig ist.
