Primfaktorzerlegung
Bei der Primfaktorzerlegung zerlegt man eine Zahl in ihre Primfaktoren. Man stellt also die gleiche Zahl als Produkt mehrerer Primzahlen dar. Man erfährt dabei viel über die Teilbarkeit der Zahl.
Beispiel: 12 = 2 · 2 · 3
Wichtig ist, dass am Ende nur noch Primzahlen übrig bleiben (die Primfaktoren). Sind noch andere Zahlen vorhanden, kann die Zahl noch weiter zerlegt werden. Für die Primfaktorzerlegung ist es sehr wichtig, schnell zu erkennen, durch welche Zahl man eine Zahl teilen kann. Die Teilbarkeitsregeln sind deshalb an dieser Stelle sehr nützlich. Diese werden im Kapitel „Teilbarkeitsregeln“ beschrieben.
Rechner Primfaktorzerlegung
Unser Lernvideo zu : Primfaktorzerlegung
Vorgehen
Man prüft der Reihe nach die Teilbarkeit der Primzahlen. Man beginnt mit der 2 und überprüft, ob die Zahl durch 2 teilbar ist. Wenn sie teilbar ist, teilt man sie durch 2 und hat damit den ersten Primfaktor gefunden. Anschließend prüft man, ob sie noch einmal durch 2 teilbar ist.
Ist das der Fall teilt man sie wieder durch 2 und erhält den nächsten Primfaktor (derselbe Primfaktor kann mehr als einmal vorkommen). Man wiederholt diesen Schritt bis die Zahl nicht mehr durch 2 teilbar ist und macht anschließend mit der nächsten Primzahl weiter.
Also mit der 3. Man prüft die Teilbarkeit durch 3 und geht nun genauso vor wie mit der 2. Anschließend kommt die 5, die 7, die 11 und so weiter. Sobald nur noch 1 übrig bleibt, ist man mit der Zerlegung fertig und hat alle Primfaktoren gefunden.
Beispiel
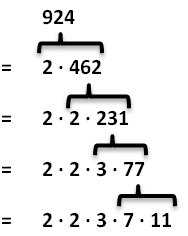
In diesem Beispiel erkennen wir zunächst, dass es sich bei 924 um eine gerade Zahl handelt, welche durch 2 geteilt werden kann. Es bleibt 2 · 462. 462 ist ebenfalls gerade und kann noch einmal durch 2 geteilt werden. Wir erhalten 2 · 2 · 231. 231 ist ungerade kann aber durch 3 geteilt werden, da die Quersumme durch 3 geteilt werden kann. Es bleibt 2 · 2 · 3 · 77. 77 kann durch 7 geteilt werden. Am Ende erhalten wir 2 · 2 · 3 · 7 · 11. Die 11 ist ebenfalls eine Primzahl und kann deshalb nicht weiter zerlegt werden. Das Ergebnis ist also 924 = 2 · 2 · 3 · 7 · 11.
Alternatives Vorgehen
Das systematische Vorgehen, welches oben vorgestellt wurde führt immer zum Ziel. Teilweise geht es allerdings etwas schneller, wenn man zunächst andere Teiler wählt. Das Endergebnis ist natürlich in beiden Fällen identisch.
Wir wollen dieses Vorgehen anhand eines Beispiels verdeutlichen:
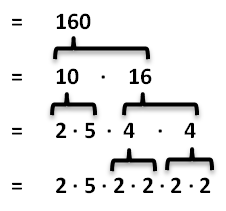
Wenn wir 160 in seine Primfaktoren zerlegen sollen, sehen wir vermutlich relativ schnell, dass sich 160 durch 10 teilen lässt. Wir können 160 also als 10 · 16 schreiben. Nun sehen wir, dass sich 10 durch 2 teilen lässt und ersetzen die 10 durch 2 · 5. Die 16 lässt sich durch vier teilen und wird durch 4 · 4 ersetzt. Natürlich hätten wir an dieser Stelle auch 16 durch 2 · 8 ersetzen können.
Das Endergebnis ist immer dasselbe. Die beiden vieren lassen sich noch jeweils durch 2 teilen und können also beide als 2 · 2 geschrieben werden. Es bleiben als Primfaktoren also fünf Mal die 2 und einmal die 5. Die Reihenfolge in der wir die Primfaktoren schreiben, ist wegen dem geltenden Kommutativgesetz egal.
Alternativ hätten wir natürlich auch systematisch vorgehen können. Das Ergebnis ist dasselbe:
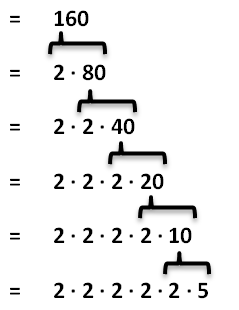
Sinn und Zweck
Wir benötigen die Primfaktorzerlegung vor allem in den folgenden Kapiteln zum Ermitteln des kleinsten gemeinsamen Teilers (ggT) und des kleinsten gemeinsamen Vielfachen (kgV).
Arbeitsblätter zu Primfaktorzerlegung
Arbeitsblatt 1 zu Primfaktorzerlegung Arbeitsblatt 2 zu Primfaktorzerlegung Arbeitsblatt 3 zu Primfaktorzerlegung Arbeitsblatt 4 zu Primfaktorzerlegung Arbeitsblatt 5 zu Primfaktorzerlegung