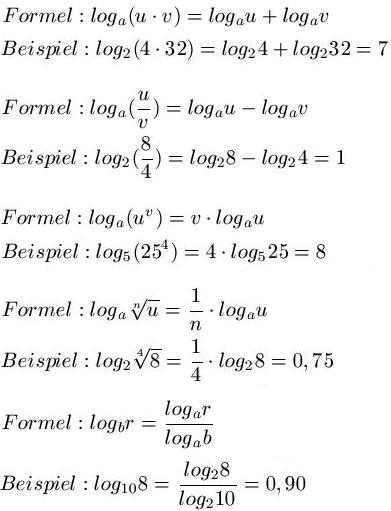Natürlicher Logarithmus
Wofür brauchen wir das Logarithmieren?
- Grundsätzlich werden Logarithmen dort verwendet, wo die Werte enorme Größen annehmen. Warum? Ganz einfach: Wenn ihr 10x in einem Koordinatensystem einzeichnet, kommt es entlang der y-Achse schnell zu Problemen, da die Werte riesig werden. Mit jedem +1 auf der x-Achse (für den Exponenten) erhöht sich der Wert enorm! 102 = 100, doch 106 = 1.000.000 ! Daher verwendet man eine logarithmische Darstellung. Anstatt 10x nutzt man also log x. Dadurch kann man bequem nur die 2 und die 6 auf der y-Achse abtragen.
Wann ist ein Logarithmus nicht definiert?
- Der Logarithmus ist nicht definiert, wenn der Numerus den Wert Null hat, da keine Potenz zum Wert Null führt (ohne Berücksichtigung von Null hoch Null):
- loga0=n.d., denn ax≠ 0
Unser Lernvideo zu : Natürlicher Logarithmus
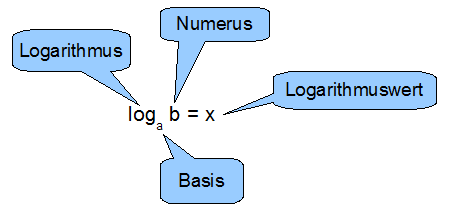
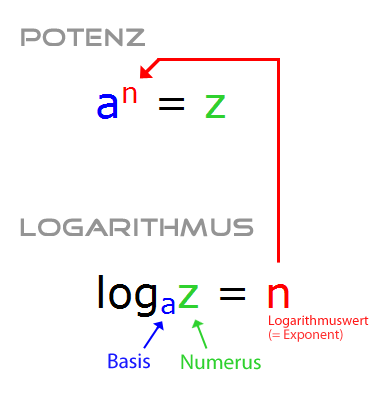
Zusammenhang zwischen Potenz und Logarithmus
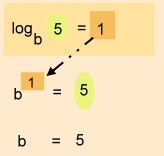
- Der Logarithmus gibt uns stets den Exponenten der Potenz an
Zudem gibt es beim Logarithmieren folgende Abkürzungen; log, lg, ln, ld
Welche Bedeutungen diese Abkürzungen?
Wahrscheinlich werdet ihr auch oft auf die Abkürzungen der Logarithmen treffen (im Zusammenhang mit der Basis). Die Kurzschreibweisenlauten:
Dekadischer Logarithmus (mit Basis 10) (auch „Zehnerlogarithmus“)
log10n = lg n
Logarithmus Naturalis (mit Basis e, Eulersche Zahl e = 2,718281828…) (auch „natürlicher Logarithmus“)
logen = ln n
Logarithmus Dualis (mit Basis 2) (auch „Zweierlogarithmus“) (wird auch als „binärer Logarithmus“ bezeichnet und mit „lb“ abgekürzt)
log2n = ld n
Merke: Der Logarithmus berechnet den Exponenten der Potenz
Beispiele
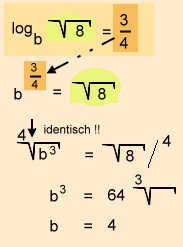
oder
Merke
loga1 = 0, denn a0 = 1
Der Logarithmus ist eins, wenn Basis und Numerus gleich sind:
logaa = 1, denn a1 = a
Die wichtigen Rechengesetze ( diese solltest du sehr gut beherrschen damit du später richtig rechnen kannst)