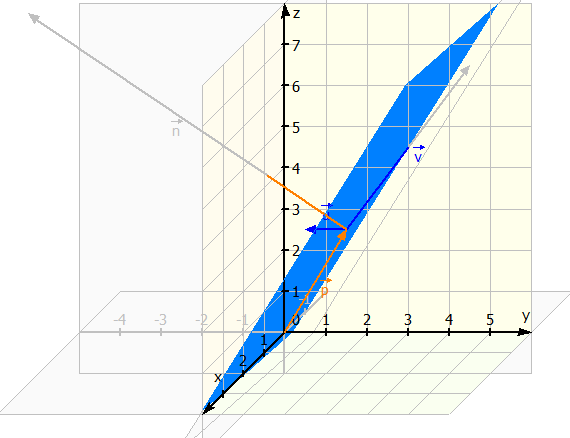
Normalenvektor einer Ebene
Die Normale einer Ebene ist ein Vektor, welcher senkrechte auf der Ebene steht. Er wird üblicherweise mit dem Buchstaben n bezeichnet.
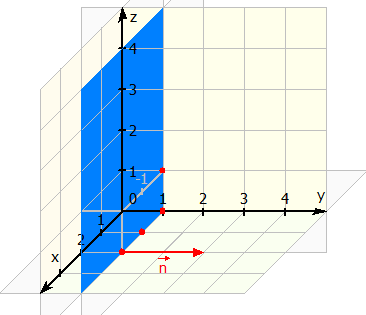
Die Normale ist dabei natürlich nicht wie auf der Zeichnung an einen Ort gebunden, sondern gibt nur die Richtung der Normalen an.
Berechnung der Normalen einer Ebene
Beispiel 1
Wir haben folgende Ebene in Parameterform gegeben:
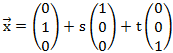
Nun wollen wir einen Vektor finden, der normal (orthogonal / senkrecht) zu der Ebene ist. Dafür muss der Vektor senkrecht zu den Richtungsvektoren (das sind die hinteren beiden) sein. Um einen Vektor zu finden, der zu diesen beiden Vektoren senkrecht ist, bilden wir das Kreuzprodukt. Das Kreuzprodukt hat als Ergebnis immer einen Vektor der orthogonal zu den beiden Ausgangsvektoren ist. Wie man das Kreuzprodukt genau bildet ist in einem anderen Artikel beschrieben.
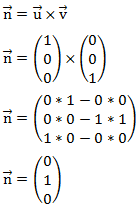
Damit haben wir den Normalenvektor gefunden.
Beispiel 2
Wir kommen nun zu einem etwas komplizierteren Beispiel. Die Ebenengleichung lautet:
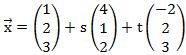
Auch hier bilden wir einfach das Kreuzprodukt der beiden Richtungsvektoren.
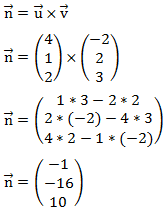
Damit haben wir einen Normalenvektor zu der Ebene gefunden.