Parametergleichung zu Koordinatengleichung
Parametergleichung
Die Ebene wird eindeutig durch 3 kolineare Punkte P1,P2,P3 definiert
Die Parametergleichung besteht aus einem Festpunkt und zwei Richtungsvektoren ,welche die Ebene aufspannen. Der Festpunkt ist der Ortsvektor von P1 . Die Richtungsvektoren erhält man, indem man die Differenz zwischen den anderen Ortsvektoren bildet
Koordinatengleichung
Die Koordinatenform ggf Koordunatengleichung ist letztlich nichts anderes als die ausmultiplizierte Version der Normalenform einer Ebene. Daher ist sie auch auf die selbe Weise aufgebaut: In der Gleichung kommt der Normalenvektor der Ebene vor, sowie ein Punkt der in der Ebene liegt. Das reicht aus, um die Ebenengleichung zu bilden. Die Koordinatenform hat den Vorteil, dass man mit ihr innerhalb kürzester Zeit ausrechnen kann, ob ein bestimmter Punkt in der Ebene liegt.
Bei der Darstellung zeigt der Stützvektor auf einen bestimmten Punkt im Raum. Von dort aus geht der Richtungsvektor ab. Dieser kann durch die Variable (lambda oder andere Buchstaben) beliebig in seiner Länge verändert werden. Dadurch kann jeder Punkt auf der Geraden bestimmt werden. Man hat also in gewisser Weise ein Koordinatensystem im Raum, bei dem der Stützvektor auf den Ursprung zeigt und von dem der Richtungsvektor abgeht – als einzige Achse des Koordinatensystems.
Das einzige was sich bei der Ebenendarstellung ändert ist, dass sozusagen eine zweite Achse dazukommt. Ist ja auch logisch, denn eine Ebene ist ja eine Fläche, nicht eine Gerade und um eine Fläche zu bestimmen, braucht man nunmal zwei Achsen. Zeichnet man ein zweidimensionales Koordinatensystem auf ein Blatt Papier, dann kann man jeden Punkt auf diesem Blatt bestimmen – man muss nur die entsprechenden x und y-Werte haben.
Vorgehensweise
♦Parameterform in ein Gleichungssystem umschreiben
♦Eine der beiden Gleichung nach λ auflösen
und in die andere einsetzen
Beispiel
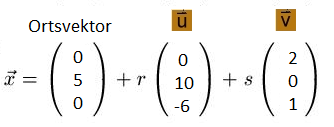
♦Es handelt sich um eine durch die Richtungsvektoren aufgespannte Ebene im dreidimensionalen Raum (ausgehend vom angegebenen Ortsvektor)
x1 = 2s
x2 = 5 +10r
x3 = -6r -s
⇒ x1 =2s | :2
⇒ 0,5 x1 = s
II) x2 = 5 +10r
III) x3 = -6r – 0,5 x1 ♦ Wir haben s= 0,5 x1 in x3 eingesetzt!
daraus folgt….
II) x2 = 5+10r I *3
III) x3 = -6r – 0,5 x1 | *5
das ergibt
II) 3x2 = 15+30r
III) 5x3 = -30r -2,5x1
Wir addieren die beiden Gleichungen und erhalten nun
⇒ 3x2 + 5x3 = -2,5x1 +15 l +2,5x1
⇒2,5x1 +3x2 +5x3 = 15 das ist unser Koordinatengleichung
