Polynomdivision
Zugegeben, schon der Name “Polynomdivison” kann einem Schrecken einflößen, besonders wenn man mit derartigen mathematischen Rechenverfahren nicht so vertraut ist. Jedoch alles halb so wild. Dieses Rechenverfahren unterscheidet sich grundsätzlich nicht von einer gewöhnlichen Division, wie wir sie alle aus dem Schulunterricht kennen, nur werden anstelle zweier Zahlen Polynome dividiert.
Die Polynomdivision wird auch Partialdivison genannt und ist ein mathematisches Rechenverfahren, das prinzipiell der bereits bekannten Division aus Grundschulzeiten gleicht. Es liegen anstatt zweier Zahlen lediglich zwei Polynome vor, die durcheinander geteilt werden.
Anwendung findet die Polynomdivision beispielsweise bei der Lösung von Gleichungen höheren Grades wie der Bestimmung von Nullstellen eines Polynoms.
Was sind Polynome?
Mehrgliedrige mathematische Ausdrücke oder Terme werden als Polynome bezeichnet. Als Term bezeichnet man sinnvolle mathematische Ausdrücke mit Zahlen, Variablen, mathematischen Symbolen und Klammern.
Ein Term ist zum Beispiel
2 + 4
a − b
7y²(x + 9)
Mit “sinnvoll” ist gemeint, dass ein mathematischer Ausdruck oder Term auch lösbar oder vollständig sein sollte. Beispielsweise -2x.(1 wäre kein sinnvoller Term, da unvollständig und nicht lösbar.
Polynome sind zum Beispiel
a + b + c
5x − x + 8x + 2x − x
−45ab + 9
Ganz wichtig:
Wenn Terme oder Polynome in mathematischen Aufgaben wie einer Division verwendet werden, müssen sie in Klammern gesetzt sein. Gerade bei der Polynomdivision ist darauf zu achten, welches Vorzeichen vor einer Klammer steht. Steht ein Minus davor, dann werden die Minuszeichen in der Klammer zu Plus, der Regelung ”zweimal Minus als Vorzeichen ergibt Plus” folgend.
Eine ausschließlich theoretische Einführung in die Thematik der Polynomdivision ist hier wenig hilfreich, weshalb wir das Verfahren direkt an einem Beispiel erläutern möchten.
Nehmen wir gleich eine ganz einfache Polynomdivision vor.
Beispiel:
x³ – x² soll dividiert werden durch x – 1, also:
(x³ – x²) : (x – 1) = ?
Wie bei einer herkömmlichen Division gehen wir dadurch vor, das x von x – 1 von dem ersten Dividenden x³ abzuziehen, wir schreiben als erstes Zwischenergebnis also x² hin:
(x³ – x²) : (x – 1) = x²
Nun kontrollieren wir dieses Zwischenergebnis, in dem wir es mit dem gesamten Divisor (x – 1) zurück multiplizieren und vom Dividenden abziehen, damit wir so den Rest berechnen und weiter rechnen können:
x² mal x ( von dem Term x – 1) ergibt x³
x² mal -1 (Minus 1, von dem Term x – 1) ergibt -x²
und auf korrekte Weise unter die Polynomdivision geschrieben sieht das so aus:
(x³ – x²) : (x – 1) = x²
– (x³ – x²)
Nicht vergessen, die Klammer mit dem Minus davor zu setzen– denn der gesamte Ausdruck muss vom Dividenden abgezogen werden. Nun subtrahieren wir:
x³ minus x³ = 0 – Null, kein Rest, wir haben also richtig gerechnet.
Dann weiter zu -x², und darunter steht -x² in der Klammer mit Minus davor, zweimal Minus bedeutet Plus, also
– x² + x² = 0 – Null, kein Rest, wir sind also schon fertig.
(x³ – x²) : (x – 1) = x²
– (x³ – x²)
0
Die Polynomdivision ist abgeschlossen, es bleibt kein Rest, und das Ergebnis lautet x².
Unser Lernvideo zu : Polynomdivision
Beispiel:
Diese etwas schwierigere Polynomrechnung kommt auch im obigen Videoclip vor:
Es sei die Funktion f(x) = x3 + x2 – 9x + 7 gegeben und x für f(x) = 0 zu bestimmen.
Mit anderen Worten ist also folgende Gleichung zu lösen:
x3 + x2 – 9x + 7 = 0
Zunächst ist es nötig, zumindest eine Lösung für x zu kennen. Ist nichts durch den Lehrer vorgegeben, bleibt nur das Ausprobieren.
Dabei fangen wir beim Raten zunächst mit 1 an, also x = 1. In diese Formel eingesetzt, ergibt das Ergebnis tatsächlich Null. Das bedeutet: In unserem Fall löst x = 1 die Gleichung.
Der Divisor für diese Polynomdivision lautet also (x – 1), weil x = 1 und (1 – 1) gleich Null ist, da es in diesem Fall ja um eine Nullstellenrechnung geht. Oder anders ausgedrückt:
Wir setzen diesen Wert für a in die Formel (x – a) ein und erhalten mit (x – 1) den Divisor für die Polynomdivison, bei der die gegebene Funktion f(x) den Dividenden darstellt.
Gehen wir nun Schritt für Schritt vor, wie wir es bereits beim ersten Beispiel gemacht haben. Zunächst notieren wir, dass x im Divisor von x³ subtrahiert x² ergibt als unser erstes Zwischenergebnis. Denn: Zunächst gilt es mit Blick auf x3 ein Vielfaches von (x – 1) zu finden, damit diese Potenz nach der ersten Subtraktion verschwindet.
(x3 + x2 – 9x + 7) : (x – 1) = x²
Zur Kontrolle müssen wir nun x² wieder zurück multiplizieren (x – 1) • x² = x3 – x² , um den ersten Substrahenden zu erhalten, und das sieht dann so aus:
(x3 + x2 – 9x + 7) : (x – 1) = x²
-(x3 + x2)
0 + 2x²
Also noch einmal zusammengefasst: Das x² wird als erster Teil unseres Ergebnisses eingetragen und wir erhalten durch die erste Subtraktion (x3 + x²) – x²3 – x²) = 2x² .
Im nächsten Schritt holen wir -9x aus dem Dividenden, schreiben dies hinter das Ergebnis der ersten Subtraktion und erhalten somit 2x2 – 9x als Minuenden der zweiten Subtraktion. Es gilt nun wieder ein Vielfaches von (x – 1) zu finden, damit nach der zweiten Subtraktion 2x2 verschwindet.
(x3 + x2 – 9x + 7) : (x – 1) = x²
-(x3 + x2)
0 + 2x² – 9x
Wir wählen 2x und multiplizieren (x – 1) • 2x = 2x2 – 2x, um den zweiten Substrahenden zu erhalten. Das 2x wird als nächster Teil unseres Ergebnisses eingetragen und wir erhalten durch die zweite Subtraktion (2x2 – 9x) – (2x2 – 2x) = -7x. Zu beachten ist das Minuszeichen vor der Klammer, aus -2x wird also Plus 2x.
(x3 + x2 – 9x + 7) : (x – 1) = x² + 2x
-(x3 + x2)
2x² – 9x
– (2x² – 2x)
0 – 7x
Im letzten Schritt holen wir +7 aus dem Dividenden, schreiben dies hinter das Ergebnis der ersten Subtraktion und erhalten somit -7x + 7 als Minuenden der dritten Subtraktion.
(x3 + x2 – 9x + 7) : (x – 1) = x² + 2x -7
-(x3 + x2 )
2x² – 9x
– (2x² – 2x)
-7x + 7
Es gilt nun wieder ein Vielfaches von (x – 1) zu finden, damit nach der dritten Subtraktion -7x verschwindet. Wir wählen -7 und multiplizieren (x – 1) • -7 = -7x + 7, um den dritten Substrahenden zu erhalten.
Das Ergebnis der letzten Subtraktion ist 0 und unsere Polynomdivision ist beendet. Das Endergebnis lautet daher x2 + 2x – 7.
Der gesamte Berechnungsprozess zusammengefasst sieht also so aus:
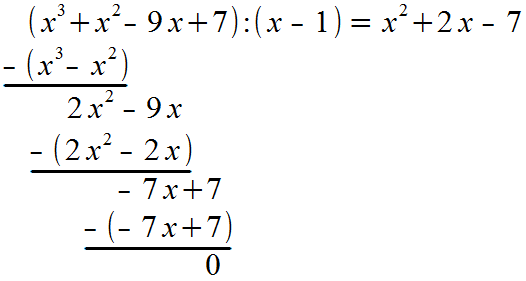
Ein weiteres Beispiel zur Übung, die einzelnen Schritte lassen wir hier einmal weg, um es sxhwieriger zu machen. Jedoch steht unten die Lösung dieser Polynomdivision, damit die einzelnen Berechnungen zum Endergebnis überprüft werden können.
(3x4 – 5×3 + 7x² – 5) : (x – 1)
Lösung:
(3x4 – 5×3 + 7x² – 5) : (x – 1) = 3x3 – 2×2 + 5x + 5 Rest: 0
– (3x4 – 3x3)
2×3 + 7x²
-(2x3 + 2x²)
5x² – 5
-(5x² – 5)
0
