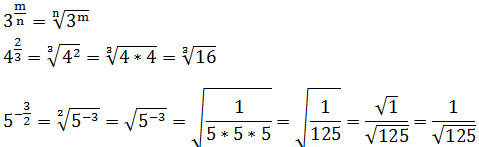Potenzen – Einführung
Die Potenz ist eine Kurzschreibweise für die Multiplikation gleicher Faktoren. Bei dieser Rechenoperation wird das wiederholte Multiplizieren eines Faktors als Potenz verkürzt:
2 * 2 = 22
2 * 2 * 2 = 23
Grundbegriffe
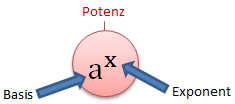
Die Basis steht unten und der Exponent oben. Das Ganze nennt man Potenz. Man spricht: „a hoch x“.
Bedeutung
ax bedeutet, dass wir die Basis a sooft mit sich selber multiplizieren, wie es der Exponent x vorgibt.
![]()
Beispiele
![]()
Eine Besonderheit ergibt sich, wenn der Exponent gleich 1 ist. Dies wird nicht notiert, denn das ist dann gleich der Basis:
![]()
Unser Lernvideo zu : Potenzen – Einführung
Definition hoch 0
Per Definition ist jede Zahl hoch 0 gleich 1. Es gilt:
![]()
Potenzen mit negativen Exponenten
Was passiert mit einer Potenz die einen negativen Exponenten hat?
Von den Begriffen her ändert sich nichts. Nur die Bedeutung ist eine andere. Denn ein negativer Exponent zeigt das die Potenz ein Divisor ist. Daher gilt:
![]()
Zu beachten ist, dass a ungleich Null sein muss! Da wir nicht durch Null teilen dürfen.
Die Berechnung ist die gleiche wie die bisher bekannte, nur dass die Potenz im Nenner steht.
Beispiele:
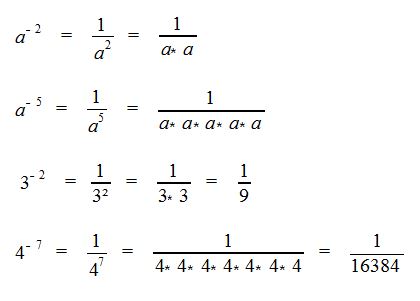
Potenzen mit rationalen Exponenten
In einer Potenz kann es auch vorkommen, dass kein ganzzahliger Exponent steht, wie wir es bisher betrachtet haben, sondern ein rationaler Exponent, also ein Bruch, wie

Hier gilten die gleichen Regeln wie bei ganzzahligen Exponenten.
![]()
Wir ziehen also die x-te Wurzel von a.
Beispiele
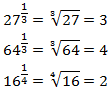
Brüche im Exponenten
Wenn sich ein Bruch (oder eine rationale Zahl) im Exponenten befindet, müssen wir alle bisherigen Fälle kombinieren. Es gilt:
![]()
Wir nehmen a also zunächst hoch m und ziehen dann die n-te Wurzel.
Beispiele