Produktregel bei Ableitungen

Formel 

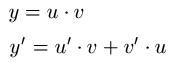
• Die Produktregel ändert sich nicht wesentlich, wenn man mehr als zwei Faktoren zum Ableiten hat.
• Wir schreiben nun statt „u(x)“ einfach „u“, statt „u'(x)“  „u‘ “ und entsprechendes für die anderen Faktoren.
• Betrachtet werden zwei Funktionen, u(x) und v(x), die differenzierbar sind. Ziel ist nun zu zeigen,daß auch das Produkt der beiden Funktionen f(x) = u(x)  v(x), und eine allgemeine Regel für die Ableitung eines Produkts herzuleiten.
• Die Produktregel führt die Ableitung eines Produktes von Funktionen auf das Modell der Ableitung der einzelnen Funktionen zurück und damit auf das Modell der Potenz- bzw. Summenregel. Man verwendet sie immer dann, wenn eine Funktion in der Form „Term mit x“ mal „Term mit x“ vorliegt.

---

---

Beispiele

f(x)= e^x+x²*e^x

Wir Klammern e^x aus

⇒f`(x)= e^x *( 1+x²)

⇒f`(x)= e^x  * (1+x²)+e^x *2x

⇒also f`(x)= e^x * (x²+2x+1)   Lösung!

f(x)= 2x³*7x²

u(x)= 2x³  ⇒ abgeleitet  u`(x)= 6x²

v(x)= 7x²  ⇒ abgeleitet v`(x)= 14x

f`(x)= 6x²* 7x²2x³ *14x      ► 42x⁴+28x⁴= 70x⁴   Lösung!

f(x)=4x⁴ * 2x³

f`(x)= 16x³ * 2x³ +4x⁴ *6x²

f`(x)= 32x⁶ +24x⁶

f`(x)= 56x⁶   Lösung!