Proportionale Zuordnung
Bei der proportionalen Zuordnung stehen zwei Mengen A und B im Verhältnis zu einander. Dabei gilt:
- Je mehr A, desto mehr B
- Bei einer Verdoppelung von A verdoppelt sich auch B
Die Werte der Mengen sind also direkt voneinander abhängig. Ein Beispiel dafür wäre zum Beispiel das Benzin, welches man an der Tankstelle kauft. Wenn man kein Benzin kauft, muss man auch nichts bezahlen, wenn man einen Liter kauft, muss man den Preis für einen Liter bezahlen. Kauft man zwei Liter, bezahlt man doppelt so viel. Kauft man viermal so viel, muss man auch viermal so viel bezahlen. Die beiden Größen sind also proportional zu einander.
Ein anderes Beispiel wäre zum Beispiel der Einkauf auf einem Markt. Wenn ich zwei Kilo Kartoffeln kaufe, bezahle ich doppelt so viel, als wenn ich nur ein Kilo Kartoffeln kaufe. Dies gilt natürlich nur, wenn es keinen Rabatt gibt, wenn ich mehr kaufe. Im Falle eines Rabatts, würde nicht mehr gelten, dass ich bei der doppelten Menge doppelt so viel bezahlen muss. Wenn es allerdings keinen Mengenrabatt gibt, ist die Zuordnung proportional.
Beim Rechnen mit proportionalen Mengen hilft einem oft der Dreisatz der es ermöglicht unbekannte Werte zu bestimmen. Dem Dreisatz haben wir einen eigenen Artikel gewidmet.
Unser Lernvideo zu : Proportionale Zuordnung
Der Proportionalitätsfaktor
Allgemein kann man eine proportionale Zuordnung folgendermaßen aufschreiben:
y = k • x
k ist dabei der Proportionalitätsfaktor. y und x sind die beiden Mengen die zueinander proportional zueinander sind.
Beispiel
Ein Liter Benzin kostet 1,50€. Wenn nun x die Liter sind und y der Preis kann man schreiben:
y = 1,50€/Liter • x
Für x setzt man also die Anzahl der Liter ein und bekommt dann den Preis raus den man dafür bezahlen muss. Der Proportionalitätsfaktor hat in diesem Fall die Einheit €/Liter. Er gibt also an, wie viel Euro man pro Liter bezahlen muss.
Den Proportionalitätsfaktor erhält man immer wenn man einen Wert der einen Menge durch den zugehörigen Wert der anderen Menge teilt. Bei jedem Wertepaar kommt man bei einer proportionalen Zuordnung auf den gleichen Wert (Den Proportionalitätsfaktor). Weichen die Quotienten voneinander ab, handelt es sich nicht um eine proportionale Zuordnung.
Grafische Darstellung: Proportionale Zuordnung
Eine Proportionale Zuordnung kann man auch sehr gut grafisch darstellen. Wir nehmen hierfür einfach die Funktion y = k • x. Diese zeichnen wir in ein Koordinatensystem. Dafür brauchen wir natürlich einen bestimmten Wert für k. Wir nehmen das Beispiel von eben. k ist also auch in diesem Beispiel 1,50 €/Liter.
Wir erstellen zunächst eine Wertetabelle. In dieser Tabelle notieren wir links mögliche Literzahlen und rechnen dann mit der Formel y = 1,50€/Liter • x den Preis aus.
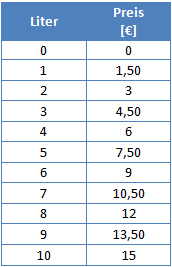
Auch bei dieser Wertetabelle gilt natürlich: Doppelte Literzahl – dopperlter Preis. Für 2 Liter bezahlt man zum Beispiel doppelt so viel wie für einen Liter. Für 6 Liter doppelt so viel wie für 3 Liter.
Mithilfe dieser Wertetabelle können wir nun diesen Graphen zeichnen.
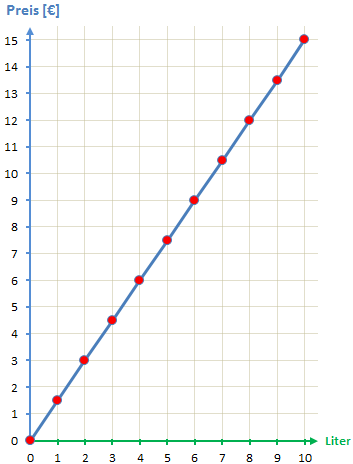
Wir haben die Liter nun auf der x-Achse (grün) und den Preis auf der y-Achse (rot) aufgetragen. Der entstandene Graph ist typisch für eine proportionale Zuordnung. Wichtig ist dabei, dass er durch den Nullpunkt beider Achsen geht (0 Liter Benzin kosten 0 Euro) und das er gerade verläuft (doppelte Literzahl, doppelter Preis). Immer wenn diese beiden Bedingungen erfüllt sind, spricht man von einer proportionalen Zuordnung.
