Höhensatz
Der Satz des Pythagoras kann uns in vielen Situationen helfen. Es gibt noch eine Erweiterung dieses Satzes und zwar den Höhensatz nach Euklid.
Wie bereits erwähnt, war Euklid ein grieschischer Mathematiker, der mit systematischer Zusammenführung allen bisherigen Wissens und neuen Erkenntnissen bis heute die Welt der Mathematik prägt.
Definition
Der Höhensatz besagt, dass in einem rechtwinkligen Dreieck das Quadrat über der Höhe dieselbe Fläche hat wie das Rechteck aus den Hypotenusenabschnitten ist.
Anders gesagt: Wenn in einem Dreieck mit den Seiten a,b und c die Höhe die Seite c in die Abschnitte q und p teilt, dann ist h² = q • p
Unser Lernvideo zu : Höhensatz
Erklärung
Zur Erläuterung schauen wir uns wieder eine Zeichnung an.
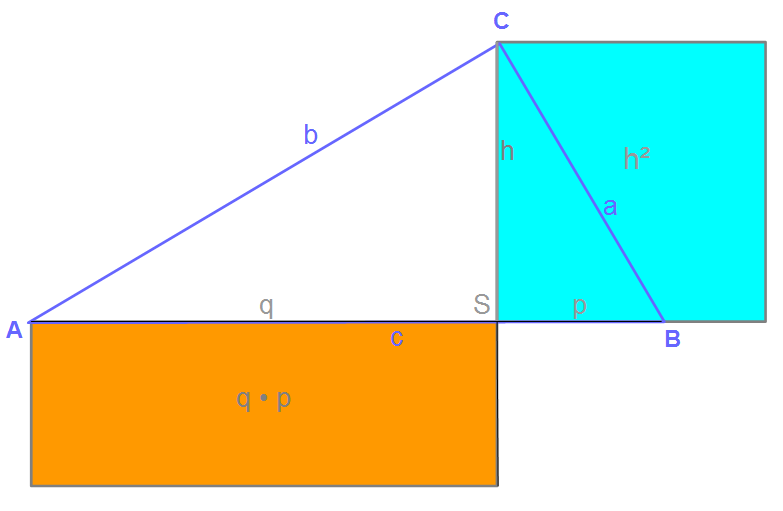
In der Abbildung seht ihr ein blaues Dreieck ABC. Dieses ist in C rechtwinklig. Die Hypothenuse ist c und das Hypothenusenquadrat c² ist hier orange eingezeichnet.
Zeichnen wir nun die Höhe des Dreiecks ein, läuft die Höhe durch den Punkt C senkrecht zur Seite c und schneidet die Seite im Punkt S uns teilt sie in zwei Abschnitte q und p. Nun ist die Strecke q von A bis S und die Strecke p von S bis B.
Der Höhensatz besagt nun, dass das Quadrat der Strecke h dieselbe Fläche hat wie q • p.
Dieses beweisen wir nun im nächsten Schritt rechnerisch.
Formel
h² = q • p
Beweis
Um den Höhensatz beweisen zu können, notieren wir zunächst alle Gegebenheiten, die wir wissen. In unserer Abbildung haben wir drei rechtwinklige Dreiecke. ABC, BCS ( 90° in Punkt S) und CAS (90° in Punkt S).
1. a² + b² = c²
2. h² + p² = a² (Abwandlung des Satzes des Pythagoras)
3. h² + q² = b² (Abwandlung des Satzes des Pythagoras)
4. q + p = c
5. (q + p)² = c²
Als erstes ersetzen wir c²:
a² + b² = (q + p)²
Dann ersetzen wir a² und b²:
h² + p² + h² + q² = (q + p)²
Nun fassen wir zusammen und lösen die binomische Formel auf
2h² + p² + q² = q² +2qp + p²
Es wird auf beiden Seiten q² und p² abgezogen
2h² = 2qp
Wir teilen durch 2
h² = q • p
Somit haben wir den Höhensatz bewiesen und können in anwenden, wenn es dazu kommt.
