Zentrische Streckung II
Im ersten Teil der Zentrischen Streckung haben wir kurz die allgemeinen Fakten erteilt und haben uns dann detailliert das Verfahren der Streckung für zwei Möglichkeiten angesehen. Einmal haben wir gelernt, wie eine Vergrößerung vollzogen wird, wenn der Streckfaktor k > 1 ist. Als zweites haben wir die Verkleinerung durch eine Streckung kennen gelernt, was der Fall ist, wenn k zwischen 0 und 1 liegt.
Nun gibt es noch eine dritte Möglichkeit. Diese trifft dann zu, wenn der Streckfaktor k kleiner als Null ist als k < 0.
Dies bedeutet, dass dann das Streckzentrum den Ursprungspunkten und den Bildpunkten liegt. Also auf der anderen Seite des Streckzentrums wird das neue Bild abgebildet. Ob das neue Bild größer oder kleiner ist als das Ursprungsbild ist wiederum davon abhängig, ob k größer oder kleiner als -1 ist.
Wenn k < -1, dann ist die Abbildung vergrößert und auf der anderen Seite von Z
wenn -1 < k < 0, dann ist die Abbildung verkleinert und auf der anderen Seite von Z
Nun schauen wir uns das Vorgehen zur Zentrischen Streckung an, wenn k < 0 ist.
Unser Lernvideo zu : Zentrische Streckung II
Streckung bei k < 0
Wie bereits oben beschrieben, bedeutet der Streckfaktor k < 0, dass das Streckzentrum zwischen Bild und Abbildung liegt. Desweiteren können wir erkennen, dass bei k < -1 die Abbildung vergrößert wird und bei k zwischen 0 und -1 wird die Abbildung verkleinert.
Wir schauen uns nun wieer ein Beispiel mit einem beliebigen Dreieck und einem beliebigen Streckzentrum an. Das Streckzentrum sei bei uns k = -1. Das bedeutet, dass die Abbildung genauso groß wie das Bild sein wird. Allerdings liegt es auf der anderen Seite des Streckzentrums.
1. Schritt: Zeichnen des Bildes und des Streckzentrums
Als erstes wird das Ursprungsbild und das Streckzentrum gezeichnet. Dies kann ganz nach Aufgabenstellung gegeben oder auch frei wählbar sein.
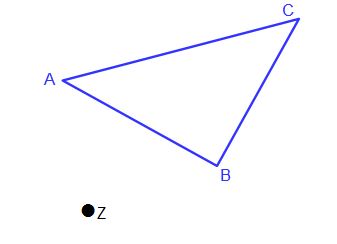
In unserem Beispiel haben wir wieder ein blaues frei gewähltes Dreieck und ein beliebiges Streckzentrum Z.
2. Schritt: Einzeichnen der HIlfsgeraden
Als nächstes werden die HIlfsgeraden ZA, ZB und ZC eingezeichnet. Diese werden zum Abmessen des Streckfaktors benötigt.
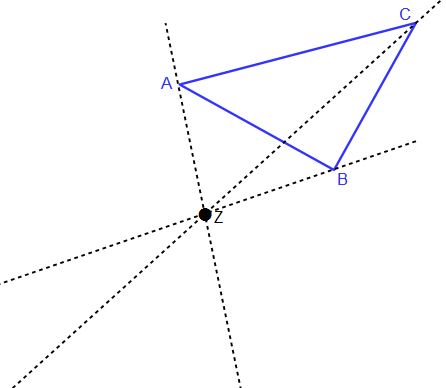
Alle Hilfslinien laufen durch das Streckzentrum Z und den jeweiligen Eckpunkten des Dreiecks. Da wir k = -1 haben wird das Abbild auf der anderen Seite von Z liegen, so dass wir auch nach dorthin die Geraden zeichnen. Was euch vielleich schon auffällt ist, dass sich die Geraden ZA und ZB kreuzen. Dadurch ist zu erwarten, dass die Bildpunkte in der Abbildung auch gekreuzt sind.
3. Schritt: Einzeichnen des Streckfaktors k
Nun setzen wir den Streckfaktor k = -1 um. dazu messen wir zunächst die Strecken Z zu den jeweiligen Eckpunkten ab.
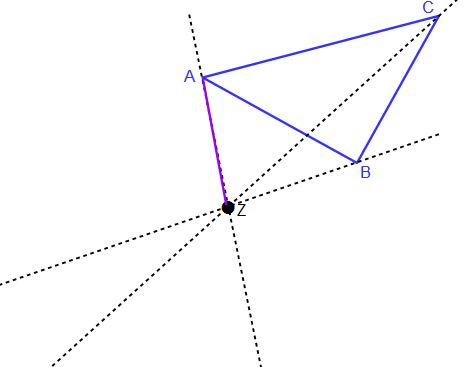
In usnerem Beispiel seht ihr die violette Strecke von Z zu A. diese hat den Faktor 1. Da wir nun k = -1 haben, können wir die selbe Streckenlänge von zu in die andere Richtung eintragen und erhalten dann den Punkt A‘.
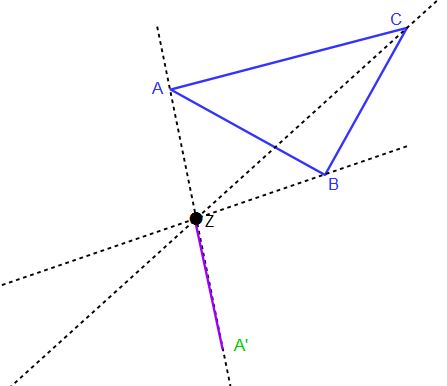
In der Abbildung seht ihr, dass wir die Streckenlänge ZA übertragen und nun den Bildpunkt A‘ ermittelt haben.
4. Schritt: Einzeichnen aller Bildpunkte
Nachdem der Bildpunkt A‘ ermittelt ist, werden nun auch die restlichen Punkte auf die selbe Weise eingetragen und die Punkte miteinader verbunden.
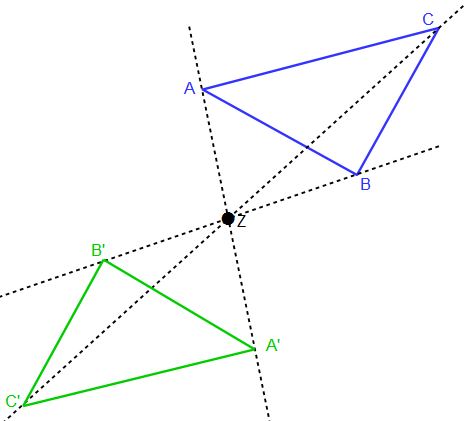
Die Abbildung zeigt, dass nun alle Punkte übertragen sind. Das neue grüne Dreieck ist genauso groß wie das blaue, allerdings wurde es gespiegelt. Dies liegt daran, dass k = -1 angegeben war. Die Strecken AB und A’B‘ sind parallel, so wie auch die anderen vergleichbaren Strecken.
Somit haben wir nun auch die dritte Zentrische Streckung durchgeführt.
Zu beachten ist nochmals, dass wenn k < -1, also -2, -3… dann wird das Dreieck vergrößert. Ist k zwischen 0 und -1, dann wird es verkleinert. Aber in beiden Fällen liegt Z zwischen dem Bild und der Abbildung.
