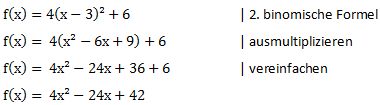Normal- und Scheitelpunktform umrechnen
Oft ist es notwendig eine gegebene quadratische Funktion von einer Darstellungsform in eine andere umzurechnen. Zum Beispiel wenn wir unterschiedliche Funktionen vergleichen wollen ist es sinnvoll diese vorher in eine einheitliche Darstellungsform zu bringen.
Von der Normalform in die Scheitelpunktform
Wenn wir eine Funktion von der Normalform in die Scheitelpunktform umformen möchten, benötigen wir die quadratische Ergänzung. Diese ist in dem gleichnamigen Kapitel erklärt. Der Einfachheit halber beginnen wir hier mit einem Beispiel bei dem der Öffnungsfaktor a gleich eins ist, er kann also weggelassen werden.
![]()
Wir beginnen also mit der Normalform:
![]()
Der erste Schritt ist die quadratische Ergänzung:
![]()
Wir ersetzen nun den ersten Teil durch die binomische Formel und erhalten dadurch bereits die Scheitelpunktform
![]()
Beim vergleich von
![]()
mit
![]()
Stellen wir fest, dass
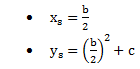
ist.
Unser Lernvideo zu : Normal- und Scheitelpunktform umrechnen
Beispiel 1
Wir möchten folgende quadratische Funktion von der Normalform in die Scheitelpunktform umformen.
![]()
Wir nehmen die quadratische Ergänzung vor. Da b hier gleich 6 ist, ergänzen wir +(6/2)² – (6/2)².
![]()
Wir berechnen:
![]()
Und erhalten dadurch:
![]()
Nun wenden wir die binomische Formel für den ersten Teil an.
![]()
Jetzt können wir vereinfachen:
![]()
Und haben damit die Funktion in die Scheitelpunktform überführt.
Beispiel 2

Beispiel 3

Bei diesem Beispiel mussten wir die zweite binomische Formel anwenden, da zwischen dem ersten und dem zweiten Teil der Funktionsvorschrift ein Minuszeichen steht.
Umrechnung mit einem vorhandenen Öffnungsfaktor a
Wenn wir einen Öffnungsfaktor a ungleich eins haben, müssen wir diesen zunächst einmal ausklammern:
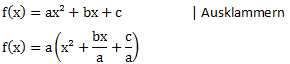
Beim ausklammern müssen wir darauf achten, dass wir jeden Summanden durch den Faktor a teilen müssen. Anschließend können wir das innere der Klammer ganz normal quadratisch ergänzen und die binomische Formel anwenden. Am Ende müssen wir dann wieder ausmultiplizieren.
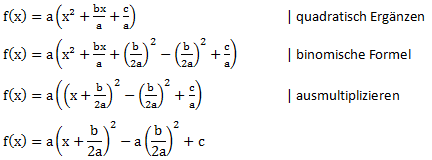
Einfacher und klarer wird es wenn wir ein Beispiel betrachten.
Beispiel

Zwischen den ausklammern und dem ausmultiplizieren des Öffnungsfaktors ist das Vorgehen also identisch mit dem vorherigen.
Von der Scheitelpunktform in die Normalform
Die Umrechnung von der Scheitelpunktform in die Normalform ist ein bisschen leichter als die umgekehrte Umrechnung, da wir hierbei keine quadratische Ergänzung benötigen, sondern nur die binomische Formel anwenden müssen.
![]()
Wir zeigen das Vorgehen zunächst allgemein und rechnen anschließend ein paar Beispiele.
Wir beginnen mit der Scheitelpunktform. Zunächst setzen wir den Öffnungsfaktor a gleich 1 damit wir diesen wegalssen können. Später zeigen wir auch wie man die Umrechnung mit einem Öffnungsfaktor durchführt.
![]()
Wir wenden die zweite binomische Formel ![]() an.
an.
Dadurch erhalten wir:
![]()
Damit sind wir bereits bei der Normalform angekommen. Wir vergleich einmal die Parameter:
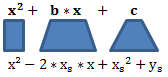
Dadurch erhalten wir:
![]()
Beispiel 1
Wir möchten folgende quadratische Funktion in die Normalform umrechnen:
![]()
Wir lösen die Klammer auf indem wir die binomische Formel anwenden:
![]()
Anschließend vereinfachen wir den Ausdruck:
![]()
Beispiel 2
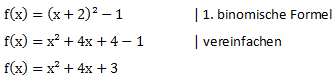
Umrechnung mit Öffnungsfaktor a
Wenn wir einen Öffnungsfaktor a in der Funktionsvorschrift haben, müssen wir das Ergebnis der binomischen Formel zunächst in Klammern schreiben und anschließend ausmultiplizieren:
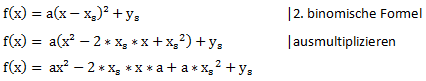
Beispiel