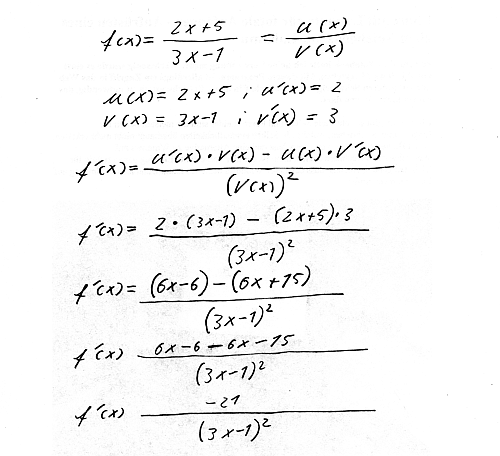Quotientenregel bei Ableitungen
►Die Quotientenregel ist eine grundlegende Regel der Differentialrechnung. Sie führt die Berechnung der Ableitung eines Quotienten von Funktionen auf die Berechnung der Ableitung der einzelnen Funktionen zurück.
►Die quotientenregel verwendet man immer bei gebrochenrationalen funktionen.
►Die Quotientenregel ist eine kombination aus Produkt und Kettenregel
Quotientenregel leitet man nach der folgenden Formel ab.
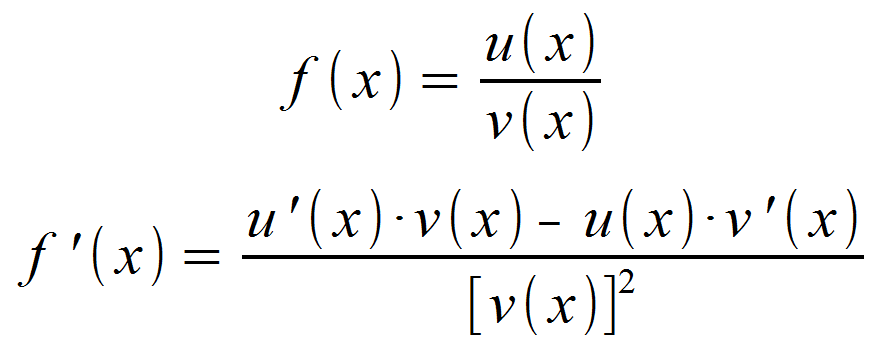
►Beachte. dass v(x) im Nenner steht. Und was im Nenner steht, darf nicht Null sein. Durch Null darf dich nicht dividiert werden!
Im Gegensatz zur Produktregel kommt es bei der Quotientenregel im Zähler auf die Reihenfolge der Terme an, da die Subtraktion nicht kommutativ (umstellbar, vertauschbar) ist! Als Eselsbrücke kannst du folgende einfache Merkregel benutzen
1. Merkregel ⇒ „NAZ minus ZAN“
Als Merkregel für den Zähler lässt sich die Kurzform „NAZ minus ZAN“ für
„Nenner („N“) mal Ableitung des Zählers („AZ“) minus Zähler („Z“) mal Ableitung des Nenners („AN“))“ benutzen.
2. Merkregel ⇒ „AZN minus ANZ“
Eine weitere Merkregel für den Zähler ist die Kurzform „AZN minus ZAN“:
Ableitung des Zählers („AZ“) mal Nenner („N“) minus Ableitung des Nenners („AN2) mal Zähler („Z“)
Vorgehensweise:
- u (x) und v (x) bestimmen
- u ‚(x) und v ‚(x) bilden- jeweils die Ableitungen!
- in Formel für f ‚(x) einsetzen
- ausmultiplizieren und vereinfachen
Beispiel
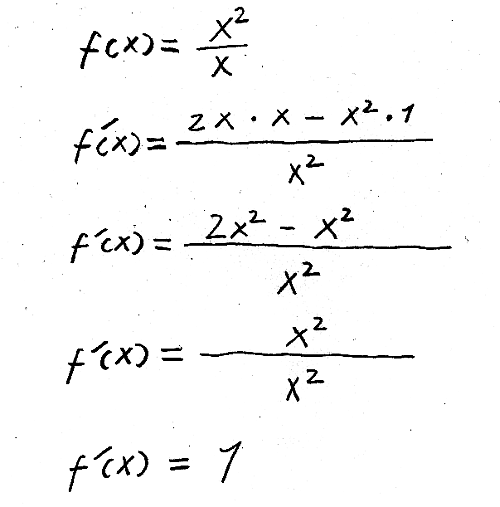
⇒ Also ist unsere erste Ableitung 1!
Beispiel 2