Sattelpunkt
Der Sattelpunkt
- Der Sattelpunkt ist eine Sonderform des Wendepunktes. Er zeichnet sich dadurch aus, dass der Graph beim Sattelpunkt augenscheinlich parallel zur x-Achse verläuft. Es bildet sich also sozusagen eine Treppenstufe.
- Der Sattelpunkt ist also ein Spezialfall eines Wendepunktes. Ein Wendepunkt ist ein Punkt, an dem der Funktionsgraph sein Krümmungsverhalten ändert.
Es gibt zwei Arten von Sattelpunkten (SP), deren Eigenschaften unten dargestellt sind.
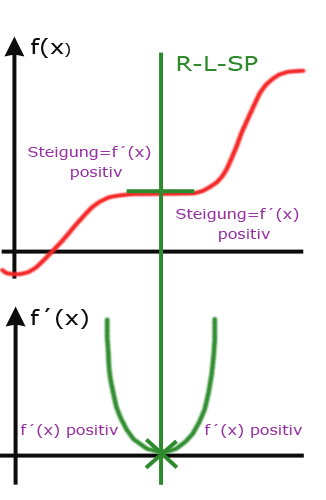
Der Rechts-Links Sattelpunkt:
Besonderheiten am R-L-SP in f(x):
- positive Steigung vorm SP
- positive Steigung nach dem SP
Daraus ergibt sich:
- Graph der Ableitungsfunktion f´(x) hat an der Nullstelle ein Minimum
- doppelte Nullstelle
- Vorzeichenwechsel der Steigung
von positiv zu positiv (VZW + +)
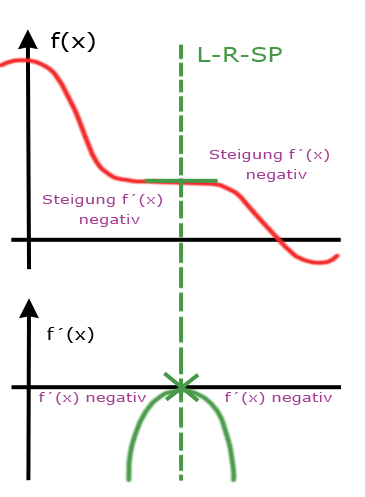
Der Links-Rechts Sattelpunkt:
Besonderheiten am L-R-SP in f(x):
- negative Steigung vorm Sattelpunkt (SP)
- negative Steigung nach dem SP
Daraus ergibt sich:
- Graph der Ableitungsfunktion f´(x) hat an der Nullstell ein Maximum
- doppelte Nullstelle
- Vorzeichenwechsel der Steigung
von negativ zu negativ (VZW – -)
Unser Lernvideo zu : Sattelpunkt
Der Sattelpunkt errechnet sich nahezu genauso wie ein normaler Wendepunkt. Daher sollte man auch zuerst nach den Wendepunkten suchen und falls es diese gibt, kann man noch überprüfen, ob die gefundenen Wendepunkte vielleicht auch Sattelpunkte sind.
Die Sattelpunkte haben die Eigenschaft, dass am Sattelpunkt für kurze Zeit die Steigung 0 herrscht – ansonsten ist alles genauso wie bei Wendepunkten. Die Bedingungen für einen Sattelpunkt sind also:
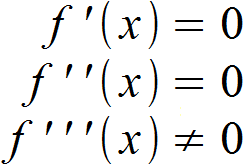
Unser Beispiel
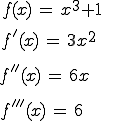
Jetzt wird erstmal nach Wendepunkten gesucht. Für diese muss gelten f “ (x) gleich 0 und f “‘ (x) ungleich 0.
Also nur die beiden letzten Bedingungen des Sattelpunktes.
![]()
![]()
Ein Wendepunkt liegt also bei x=0.
Jetzt wird noch geprüft, ob dieser Wendepunkt vielleicht ein Sattelpunkt ist.
Dazu wird der x-Wert (also 0) in die 1. Ableitung eingesetzt (f ‚ (x)).
Ist das Ergebnis gleich Null, dann ist dieser Punkt ein Sattelpunkt, ansonsten nur ein ganz normaler Wendepunkt.
![]()
Die erste Ableitung ist also für diesen Wendepunkt 0.
Damit sind alle drei Bedingungen eines Sattelpunktes erfüllt – der Punkt ist ein Sattelpunkt.
Nun rechnet man noch schnell die zugehörige y-Koordinate zur x-Koordinate aus, damit man den Punkt genau im Koordinatensystem bestimmen kann:
![]()
Der Sattelpunkt liegt also bei (0 | 1)
Merke Dir
Zweite Ableitung berechnen
- Nullstellen der zweiten Ableitung berechnen
- Dritte Ableitung berechnen
- Die in Schritt 2 berechneten x-Werte in die dritte Ableitung einsetzen
-> ist die dritte Ableitung dann ungleich Null, handelt es sich um einen Wendepunkt - Die in Schritt 2 berechneten x-Werte in die erste Ableitung einsetzen
-> ist die erste Ableitung dann gleich Null, so handelt es sich um einen Sattelpunkt - Die x-Werte in die Funktion f(x) einsetzen, um die y-Koordinaten der Sattelpunkte zu berechnen
