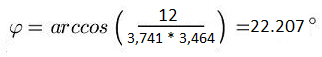Schnittwinkel zweier Geraden
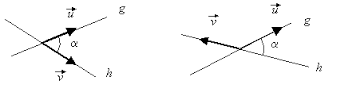
Der Schnittwinkel zweier Geraden ist immer der kleinere der beiden Winkel, welchen die Geraden miteinander bilden. Es gilt: 0°< φ ≤ 90°
Eine Gerade schließt mit einer Koordinatenachse zwei Winkel ein. Unter dem Schnittwinkel einer Geraden mit einer Achse versteht man den kleineren der beiden möglichen Winkel; er wird stets positiv angegeben. Bei einer positiven Steigung stimmt der Schnittwinkel mit der x-Achse mit dem Steigungswinkel überein.
Der Schnittwinkel zweier Geraden im Raum kann demzufolge höchstens 90° betragen. In diesem Grenzfall heißen g1 und g2 zueinander senkrecht bzw. orthogonal
Formel für den Schnittwinkel
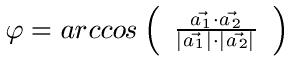
Vorgehensweise
- Skalarprodukt der Richtungsvektoren berechnen
- Länge der Richtungsvektoren berechnen
- Zwischenergebnisse in die Formel einsetzen
- Formel nach φ auflösen
Voraussetzung
Ein Schnittwinkel existiert nur, wenn die beiden gegebenen Geraden eine unterschiedliche Steigung besitzen. Dies ist nämlich die Voraussetzung dafür, dass sich die Geraden schneiden.
Beispiel
Gegeben haben wir folgende Geraden
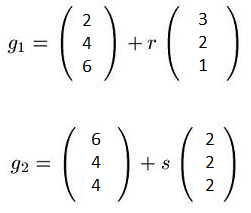
Wir berechnen jetzt das Skalarprodukt der Richtungsvektoren
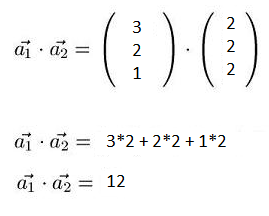
Nun berechnen wir die Länge der Richtungsvektoren
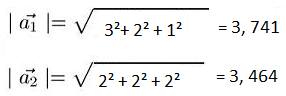
Jetzt das Zwischenergebnisse in die Formel einsetzen