Sehnenviereck
Unter einem Sehnenviereck versteht man ein Viereck, dessen Eckpunkte alle auf einem Kreis liegen. Dies ist der Umkreis des Vierecks. Die einzelnen Kanten sind Sehnen des Kreises, wodurch der Name Sehnenviereck bestimmt ist. Ein Sehnenviereck kann sowohl ein „normales“ (konvexes) als auch ein überschlagenes (konkaves) Viereck sein.
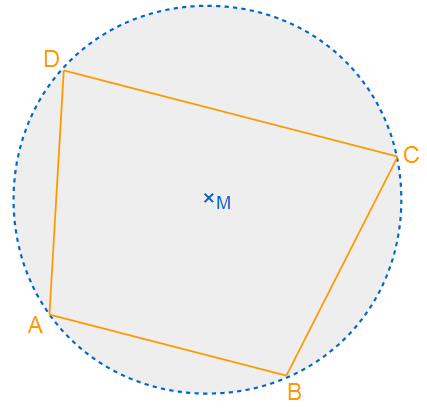
Wir habn hier ein oranges Viereck mit den Eckpunkten ABCD. Alle Punkte liegen auf dem gestrichelten Kreis mit dem Mittelpunkt M. Der Kreis ist der Umkreis des Vierecks.
Besonderheiten im Sehnenviereck
Im Sehnenviereck finden wir einige Besonderheiten, die sich durch den Fakt der Sehnen ergeben.
Winkelsatz
Im Sehnenviereck gilt, dass die gegenüberliegende Winkel summiert 180° ergeben. Das bedeutet:
α + γ = 180°
β + δ = 180°
Dieser Satz ist umkehrbar. Darunter versteht man, dass wenn in einem Viereck die beiden gegenüberliegende Seiten 180° summiert 180° ergeben, handelt es sich um ein Sehnenviereck. Das bedeutet somit auch, dass jedes Quadrat und jedes Rechteck auch einen Sehnenviereck ist und einen Umkreis hat. Der Beweis dazu finden wir im Kreiswinkelsatz, den ihr auch auf unserer Homepage finden könnt. Dieser Winkelsatz gilt nur bei konvexen Vierecken nicht bei überschlagenen.
Satz des Plotemäus
Plotemäus war ein griechischer Mathematiker, Astronom und Philosoph. Nach ihm wurde dieser Satz benannt, der das Verhältnis der Seiten und der Diagonalen im Sehnenviereck beschreibt. Im Sehnenviereck ist das Produkt der Diagonalen e und f genauso groß wie die Addition der Produkte der gegenüberliegende Seiten:
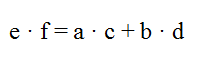
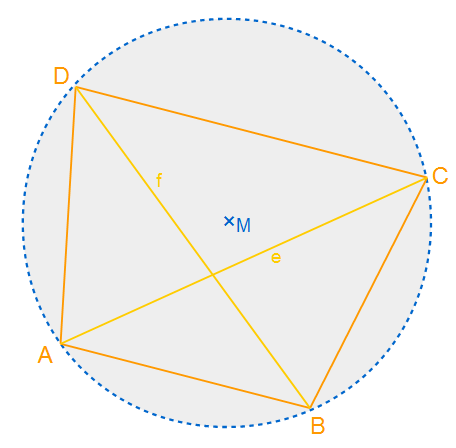
In der Zeichnung sehen wir nochmal die Diagonalen des Vierecks e und f. Nach der Formel ist das Produkt von e und f genauso lang wie die Summe von a•c und b•d. Die Formel ist natürlich umstellbar, so dass man einzelne Längen ermitteln kann. Auch dieser Satz gilt nicht bei überschlagenen Vierecken.
Mittelpunkt des Umkreises
Verbinden wir alle Eckpunkte ABC und D des Sehnenvierecks mit dem Mittelpunkt des Umkreises erhalten wir vier gleichschenklige Dreiecke. Dieses liegt daran, dass der Mittelpunkt von jedem Eckpunkt die Entfernung des Radiuses hat und somit die Schenkel vom Mittelpunkt zu den Eckpunkten alle gleich sind.
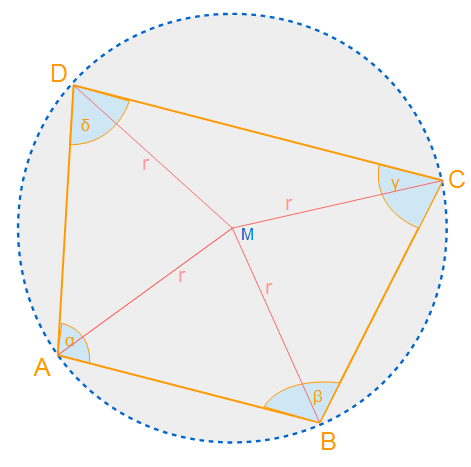
In der Abbildung sehen wir das Sehnenviereck ABCD. Die Eckpunkte sind mit M verbunden. Die Entfernung vom Eckpunkt zu M hat die Streckenlänge r. Somit ist z.B. ABM und CDM gleichschenklige Dreiecke.
