Sinussatz
Der Sinussatz
Was ist der Sinussatz?
Der Sinussatz ist das Verhältnis der Längen zweier Seiten gleich dem Verhältnis der Sinuswerte ihrer gegenüberliegenden Winkel
Also können wir den Sinussatz folgendermaßen definieren.
In jedem Dreieck gilt: Der „Sinus eines Winkels“ zu seiner gegenüberliegenden Seite ist gleich dem „Sinus eines zweiten Winkels“ zu seiner gegenüberliegenden Seite.
Durch Umformungen kann man den Sinussatz auch auf folgende Formen bringen:
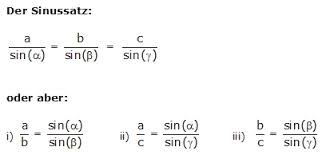
Dazu berechnen wir ein Beispiel
Wir wollen mit dem Sinussatz die Seitenlängen berechnen. Folgendes Dreieck haben wir gegeben.
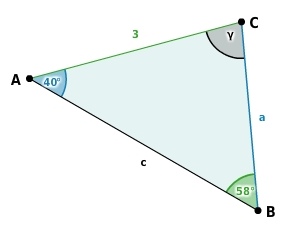
Nun wir wissen, dass wir aus zwei Winkeln und einer Seite die restlichen ebenfalls berechnen können.
Wir wollen also die Länge a berechnen.

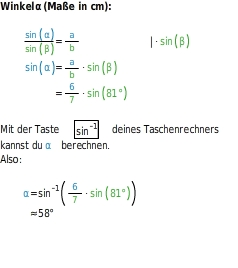
Nun wollen wir noch einen Beispiel für die Winkelberechnung durchführen. Wir haben das folgende Dreieck mit folgenden Werte zur Verfügung
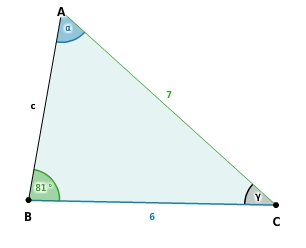
Wie man bei einem Sinussatz die Winkeln berechnet hatten wir bei der Einleitung oben erklärt. Bzw. Welche der folgenden Formeln wann benutz wird. In unserem Beispiel haben wir zwei Seiten und einen Winkel gegeben. Die Formel wird so umgestellt, dass wir am Ende nur noch sin (α) haben.
Unser Lernvideo zu : Sinussatz
Merke dir!
Der Sinussatz ist anwendbar wenn:
- zwei Winkel und eine Seite gegeben sind
- zwei Seiten und ein Winkel gegeben sind, wobei der Winkel nicht von den zwei gegebenen Seiten eingeschlossen werden darf
Winkel und Verhältnisse
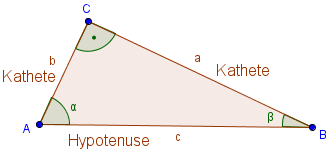
- Der “ Sinus“ eines Winkels im rechtwinkligen Dreieck ist das Verhältnis aus Gegenkathete zu Hypotenuse.
- Der “ Kosinus“ eines Winkels im rechtwinkligen Dreieck ist das Verhältnis aus Ankathete zu Hypotenuse.
- Der “ Tangens“ eines Winkels im rechtwinkligen Dreieck ist das Verhältnis aus Gegenkathete zu Ankathete.
,Was haben wir also gelernt?
Wir haben gelernt, dass der Sinussatz in jedem Dreieck gilt! Er gilt also im spitzwinkligen, rechtwinkligen und im stumpfwinkligen Dreieck!!!
Gibt es Ausnahmen?
Ja gibt es! Es gibt Dreiecke, die nicht mit dem Sinussatz berechnet werden können. Es gibt jedoch zwei Situationen, in den man den Sinussatz nicht anwenden kann. Zwei Seiten und ein Winkel sind bekannt, jedoch ist der bekannte Winkel eingeschlossen. Alle drei Seiten sind bekannt, jedoch kein Winkel!
Bei der ersten Situation muss man zunächst die unbekannte Seite ermitteln, sind alle 3 Seiten, jedoch kein Winkel bekannt, braucht man den Wert eines unbekannten Winkels. Hierfür kann der Kosinussatz angewendet werden. Hat man den Wert der unbekannten Seite bzw. vom unbekannten Winkels ermittelt, kann man danach mit den Sinussätzen die übrigen fehlenden Werte ermitteln.
kleiner Tipp: Beginne beim Sinussatz immer mit dem gesuchten Stück . Die Umstellung der Formel ist dann viel leichter!,
Interessante Fragen und Antworten zu Sinussatz
Weshalb darf Sinus im Sinussatz nicht gößer als 1 sein? |
| Da die allgemeine Formulierung des Sinussatz wie folgt lautet: a: b: c = sin (?) : sin (?) : sin (?), verteilen sich die Längen zweier Seiten in einem Dreieck, wie die Sinuswerte der gegenüberliegenden Winkel. Somit wird in diesem Satz ausgesagt, dass Sinus = Gegenkathete / Hypotenuse ist. Eine Hypotenuse wird als längste Seite in einem rechtwinkligen Dreieck bezeichnet, weil diese dem rechten Winkel (der rechte Winkel ist der größte Winkel) gegenüberliegt. Folglich ist die Kathete die kürzere Seite. Somit ist die Hypotenuse immer die längere Seite der Gegenkathete. Da bei der Berechnung von Sinus, die Hypotenuse im Nenner steht und die Gegenkathete im Zähler, kann Sinus nicht größer sein als 1. Da der Nenner größer ist als der Zähler. |
Wie ermittelt man Seiten oder Winkel eines dreiecks mit dem Sinussatz? |
Der Sinussatz stellt in der Trigonometrie eine Beziehung zwischen den gegenüberliegenden Seiten eines allgemeinen Dreiecks und den Winkeln her.
Die Formeln:Die Längen von zwei Seiten in dem Dreieck verhalten sich wie die Sinuswerte der Winkel die gegenüberliegen. Somit ist a / sin (alpha) = b / sin (beta) = c / sin (gamma). Der Sinussatz wird häufig auch als Verhältnisgleichung ausgedrückt. Diese sieht wie folgt aus: a : b : c = sin (alpha) : sin (beta) : sin (gamma). Ein Beispiel:Ein Dreieck hat folgende bekannte Größen: die Längen a = 5 cm und b = 4 cm. Außerdem ist der Winkel alpha = 70° bekannt. Der Winkel beta ist unbekannt und soll mithilfe des Sinussatz berechnet werden. Dem Text werden folgende Angaben entnommen: a = 5 cm b = 4 cm Winkel alpha = 70° gesucht wird: Winkel beta Diese Angaben werden in die Formel des Sinussatz eingegeben: Formel: a / sin (alpha) = b / sin (beta). sin (beta) = (b / a) x sin (alpha) |
Wie kann man den Sinussatz beweisen? |
| Um den Sinussatz herzuleiten wird Wissen zu den Winkelfunktionen benötigt. Die Höhe hc zerlegt ein Dreieck in zwei Teildreiecke die rechtwinklig sind. In diesen Teildreiecken können die Sinuswerte von alpha und beta je als Quotient von Hypotenuse und Gegenkathete ausgedrückt werden. Die Sinuswerte werden zunächst als Quotient aus der Hypotenuse und der Gegenkathete ausgedrückt. Anschließend werden diese der Höhe nach umgestellt und dann gleichgesetzt. Die gewohnte Schreibweise wird durch das Umformen erhalten.In der Formel ausgedrückt:
sin (alpha) = hc (die Höhe) / b daraus ergibt sich: hc = b x sin (alpha) somit ist: a x sin (beta) = b x sin (alpha) hieraus folgt der Sinussatz: a / sin (alpha) = b / sin (beta) |
