Steigende Monotonie
- Wir wollen jetzt also klären, wann steigt die Funktion an und wann fällt sie. Für die Steigung an jedem Punkt der Funktion haben wir die Ableitungsfunktion. Wenn die Ableitungsfunktion einen positiven Wert hat, dann steigt unsere Funktion an. Wenn die Ableitungsfunktion einen negativen Wert hat, dann fällt unsere Funktion. Um also eine Aussage darüber zu treffen, in welchen Intervallen die Funktion steigt und fällt, untersuchen wir die Ableitungsfunktion auf positive Werte und negative Werte, genau genommen auf die Stellen, an denen sie von positiv zu negativ wechselt. Und das heißt nichts anderes, dass wir die Nullstellen der Ableitungsfunktion suchen, dann gucken, sind links von der ersten Nullstelle von links die Werte positive Ableitungsfunktionswerte, dann steigt bis dahin der Funktionsgraph. Dann sehen wir, ob rechts von dieser Nullstelle die Werte positiv oder negativ sind und entscheiden so, ob sie weiter steigt oder ob sie fällt
Monotonie bei Zahlenfolgen
►Eine streng monoton steigende Zahlenfolge ist: 2, 3, 5, 8, 10, 20
Es gilt, dass jedes Folgeglied größer ist als das vorige: 2 < 3 < 5 < 8 < 10 < 20
►Eine monoton steigende Zahlenfolge ist: 3, 5, 5, 5, 20, 110
Es gilt, dass jedes Folgeglied größer gleich dem vorigen ist: 3 < 5 = 5 = 5 < 20 < 110
►Eine streng monoton fallende Zahlenfolge ist: 20, 10, 8, 5, 3, 2
Es gilt, dass jedes Folgeglied kleiner ist als das vorige: 20 > 10 > 8 > 5 > 3 > 2
►Eine monoton fallende Zahlenfolge ist: 110, 20, 5, 5, 5, 3
Es gilt, dass jedes Folgeglied kleiner gleich dem vorigen ist: 110 > 20 > 5 = 5 = 5 > 3
Nach dieser Logik könnt Ihr das Monotonieverhalten einer Funktion untersuchen!
Unser Lernvideo zu : Steigende Monotonie
MonotonieSatz
Die Funktion f sei im Intervall differenzierbar. Wenn für alle x aus I gilt:
f`(x) > 0, dann ist f streng monoton wachsend in I.
f`(x) < 0, dann ist f streng monoton fallend in I.
Die Funktion f ist streng monoton steigend, wenn f`(x) >0 gilt.
Die Funktion f ist streng monoton fallend, wenn f`(x) <0 gilt.
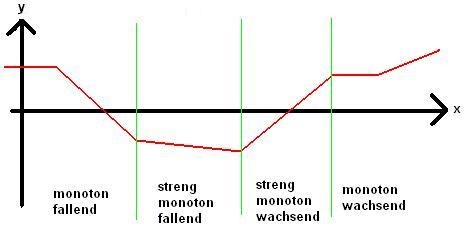
Grundsätzlich gibt es zwei unterschiedliche Herangehensweisen, um das Monotonieverhalten einer Funktion zu bestimmen.
Verfahren 1
Beim ersten Verfahren ist es notwendig, die zweite Ableitung zu berechnen.
- Erste Ableitung berechnen
- Nullstellen der ersten Ableitung berechnen
- Zweite Ableitung berechnen
- Nullstellen der ersten Ableitung in die zweite Ableitung einsetzen
- Intervalle benennen
Verfahren 2
Beim zweiten Verfahren ist es nicht notwendig, die zweite Ableitung zu berechnen.
- Erste Ableitung berechnen
- Nullstellen der ersten Ableitung berechnen
- Intervalle benennen
- Monotonietabelle aufstellen
- Vorzeichen der Intervalle berechnen
Merke
►Das Monotonieverhalten einer Funktion beschreibt den Verlauf des Graphen der Funktion, es sagt aus ob die Funktion steigt, fällt oder konstant ist.
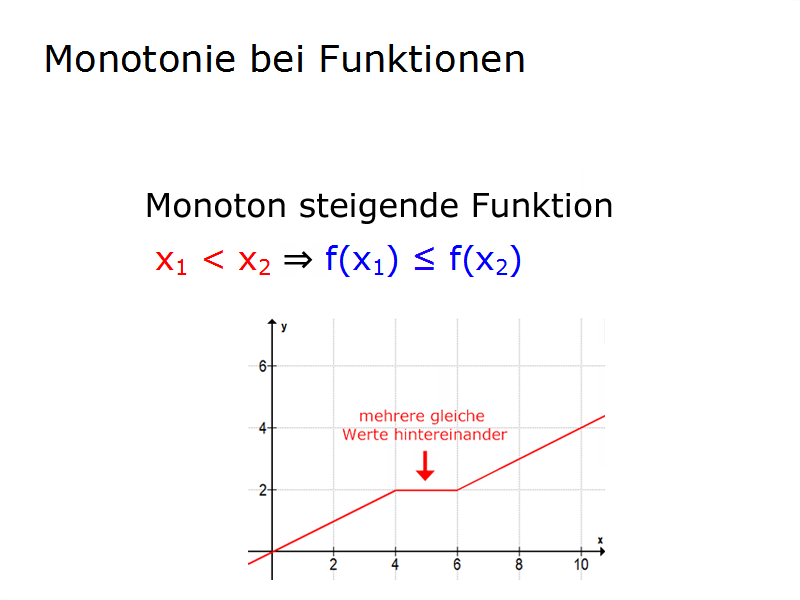
►Eine Funktion ist monoton steigend (auch monoton wachsend genannt) wenn sie immer größer wird oder konstant bleibt jedoch nie kleiner wird.
►Eine Funktion ist monoton fallend wenn sie immer kleiner wird oder konstant bleibt jedoch nie größer wird.
►Wenn eine Funktion weder fällt, noch steigt, dann nennt man sie konstant
