Steigung und y-Achsenabschnitt
Bei der Grundfunktion f(x) = a • x + b ist
- a die Steigung und
- b der y-Achsenabschnitt.
Man bezeichnet diese beiden „Stellschrauben“ als Parameter der linearen Funktion.
Unser Lernvideo zu : Steigung und y-Achsenabschnitt
Steigung
Die Steigung a gibt an wie steil die Gerade verläuft. Oft wird die Steigung auch mit anderen Buchstaben bezeichnet. Weit verbreitet ist auch die Variable m als Steigung. Ist die Zahl groß, ist die Gerade sehr steil, ist die Zahl klein, verläuft die Gerade flach.
Der Wert der Steigung gibt an um wieviel der y-Wert wächst wenn der x-Wert um 1 erhöht wird. Wenn die Steigung beispielsweise a=2 ist, dann bedeutet das, dass bei einer Erhöhung des x-Werts um 1, der y-Wert um 2 erhöht wird. Sehr gut zu sehen ist das mit Hilfe des Steigungsdreiecks:
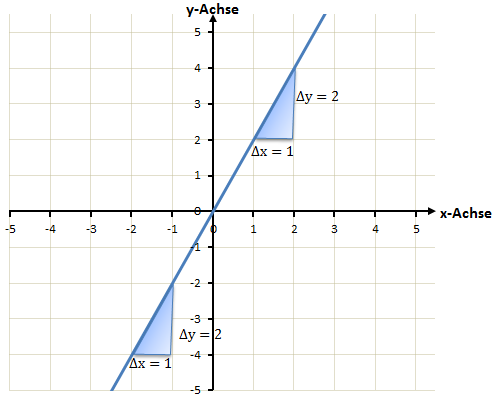
Egal wo wir das Steigungsdreieck zeichnen. Wenn die x-Differenz (Δx) gleich 1 ist, ist bei einer Steigung von 2 auch die y-Differenz (Δy) gleich 2. Dies kann uns natürlich auch das Zeichnen einer linearen Funktion erheblich erleichtern, da wir bereits wissen, wie steil die gerade verlaufen muss.
Um einen besseren Eindruck von verschiedenen Steigungen zu erhalten hier ein paar Beispiele. Wir variieren die Variable a und setzen die Variable b gleich 0:
- f(x) = 0,2 • x
- g(x) = 0,5 • x
- h(x) = 1 • x
- i(x) = 3 • x
- j(x) = -2 • x
Die Funktionen sehen folgendermaßen aus:
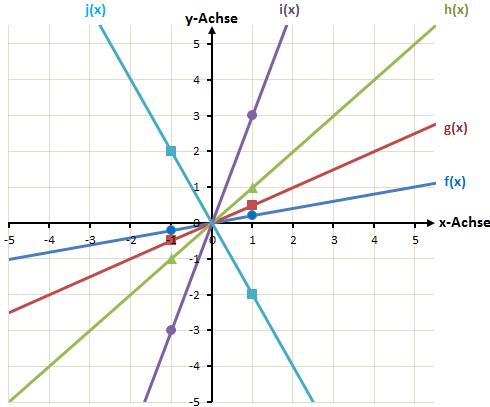
Da bei allen Funktionen b = 0 ist, verlaufen sie alle durch den Nullpunkt.
Sie haben aber verschiedene Steigungen.
i(x) hat die Steigung 3 und verläuft am steilsten.
f(x) dagegen hat eine geringe Steigung und verläuft sehr flach.
j(x) ist die einzige Funktion mit einer negativen Steigung. Eine negative Steigung bedeutet, dass die Funktion in positiver x-Richtung (nach rechts) immer kleinere y-Werte besitzt, es ist also eine fallende Gerade.
y-Achsenabschnitt
Das b gibt den y-Achsenabschnitt an. Dies ist der Schnittpunkt mit der y-Achse. Man kann mit diesem Parameter die lineare Funktion nach unten oder oben verschieben. Mit einem positiven Wert verschiebt man die Funktion nach oben, mit einem negativen Wert nach unten.
Wenn man die Funktion einer linearen Funktion sieht, kann man also den Schnittpunkt mit der y-Achse sofort ablesen. Man kennt also schon einen Punkt durch den die Gerade verläuft. Dieser ist immer P(0/b).
Beispiele y-Achsenabschnitt
Wir setzen jetzt a auf den Konstanten Wert 0,5 und variieren b:
- f(x) = 0,5 • x – 2 y-Achsenabschnitt b = -2
- g(x) = 0,5 • x – 1 y-Achsenabschnitt b = -1
- h(x) = 0,5 • x y-Achsenabschnitt b = 0
- i(x) = 0,5 • x + 2 y-Achsenabschnitt b = 2
Wenn wir die Funktionen zeichnen erhalten wir folgendes Bild:
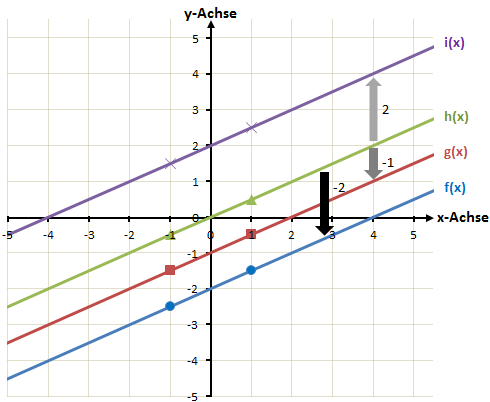
Wir sehen, dass alle vier Funktionen parallel verlaufen. Sie haben also alle die gleiche Steigung.
Genau das war ja auch unsere Absicht als wir den Parameter a bei allen Funktionen auf 0,5 gesetzt haben. Da wir b aber verändert haben, sind die Funktionen nach oben oder unten verschoben.
i(x) beispielsweise wurde um 2 nach oben verschoben und verläuft nun durch den Punkt P(0/2).
h(x) wurde nicht verschoben und verläuft deshalb durch den Ursprung des Koordinatensystems P(0/0).
g(x) wurde um 1 nach unten verschoben und verläuft nun durch P(0/-1) und f(x) wurde um 2 nach unten verschoben.
Der y-Achsenabschnitt von f(x) ist also -2 beziehungsweise P(0/-2).
