Summe ableiten
Bevor wir auf die Ableitungsregel kommen, schauen wir uns einmal den Beweis der Ableitung an.
Diese besagt folgendes

►somit haben wir unser Summenregel bewiesen!
- Nachdem wir die Summenregel mathematisch beweisen haben kommen wir auf die Formel. Summen leitet man nach dieser Formel ab
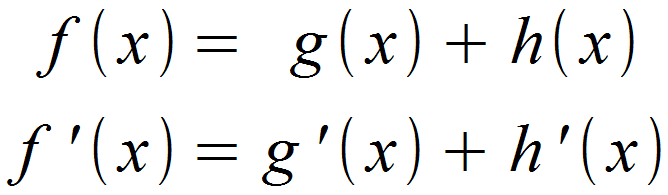
Wichtig: Summen leitet man immer dann ab, wenn zwei Funktionen durch ein Pluszeichen (+) getrennt sind!
Beispiele
- f(x)= e5x+4*e3x
- f`(x)=5e5x+ 12e3x
- f(x)=4x3+3x2
- f(x)=12x2+6x
weitere Beispiel Anwendungen
h(x)= x+1
f(x)= x
g(x)= 1
f`(x)= 1
g(x9= 0
h`(x)= 1 +0 =1 ►Lösung ⇒ hier haben wir teilweise abgeleitet, Schritt für Schritt!
weitere Beispiele…
- f(x)= 3x2+5x
- f`(x)= 6x+5
Merke
►Die Summenregel ermöglicht es sehr leicht summierte Funktionen in einfachere Konstrukte zu zerlegen.
►Besteht eine Funktion aus mehreren Termen, so werden diese als einzelne Funktionen betrachtet und können auch einzeln abgeleitet werden.
►Die Summenregel ist in der Mathematik eine der Grundregeln der Differentialrechnung. Sie besagt, dass die Summe aus zwei differenzierbaren Funktionen wieder differenzierbar ist und dass eine solche Summe aus Funktionen gliedweise differenziert werden kann.
►Die Summenregel gilt auch für mehr als zwei Summanden, was mithilfe des Beweisverfahrens der vollständigen Induktion bewiesen werden kann.
