Transponierte Matrix

Eine transponierte Matrix wird auch gespiegelte oder gestürzte Matrix genannt. Man erhält sie durch Vertauschen der Zeilen und Spalten einer Ausgangsmatrix. So bildet die erste Spalte der Ausgangsmatrix also die erste Zeile der transponierten Matrix, die zweite Spalte der Ausgangsmatrix die zweite Zeile der transponierten Matrix und so weiter. Die Bildung der transponierten Matrix wird Transponierung, Transposition oder Stürzen genannt und kann auch als Spiegelung der Ausgangsmatrix an ihrer Hauptdiagonalen gesehen werden.

Als Beispiel sei hier eine (2,3)-Matrix A aufgeführt, dessen transponierte Matrix eine (3,2)-Matrix mit folgenden Elementen ist:

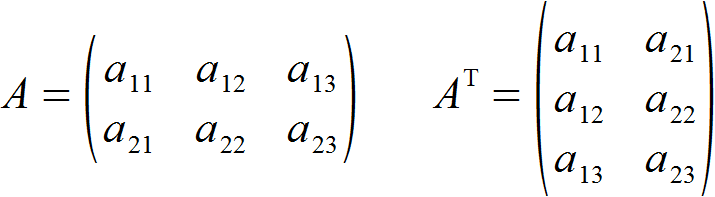
• Die Ausgangsmatrix muss keine Bedingungen erfüllen, jede Matrix ist transponierbar.
• Die transponierte Matrix einer transponierten Matrix entspricht wieder der Ausgangamatrix.
  (A^T)^T = A
• Transponiert man eine Matrizensumme, so entspricht dies der Summe der einzeln transponierten Matrizen.
  (A + B)^T = A^T + B^T
• Ebenso entspricht ein transponiertes Matrizenprodukt dem Produkt der einzeln transponierten Matrizen, jedoch in vertauschter Reihenfolge.
  (A · B)^T = B^T · A^T

Beispiel

Die folgende Matrix A soll transponiert werden.

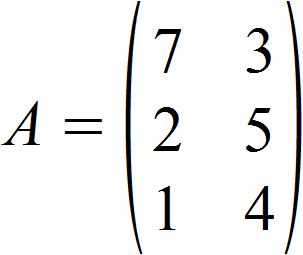
Zur Veranschaulichung wurden die Spalten der Ausgangsmatrix A unterschiedlich gefärbt. Wir gehen also zunächst die erste Spalte, hier grün dargestellt, von oben nach unten entlang und tragen die Elemente von links nach rechts in die erste Zeile der transponierten Matrix ein. Ebenso verfahren wir mit der zweiten Spalte der Ausgangsmatrix, hier violett eingefärbt, und bekommen so die zweite Zeile der transponierten Matrix.

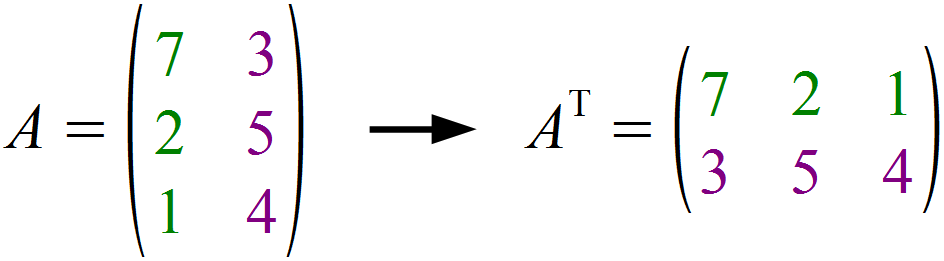
Da die Ausgangsmatrix eine (3,2)-Matrix ist, erhalten wir bei der Transponierung somit eine (2,3)-Matrix.