Kreissektor
Ein Kreissektor ist ein Teilstück eines Kreises. Dieser Teilbereich wird von 2 Radien und einem Kreisbogen b begrenzt und wird auch als Kreisausschnitt bezeichnet
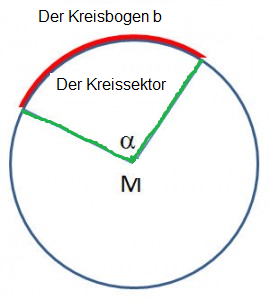
Eigenschaften des Kreissektors
•Teilfläche einer Kreisfläche, die von einem Kreisbogen (b) und zwei Kreisradien (r) begrenzt wird.
•Der Zentriwinkel α hat seinen Scheitel im Kreismittelpunkt
•Bei einem Halbkreis beträgt der Zentriwinkel α 180°, bei einem Viertelkreis 90°
Unser Lernvideo zu : Kreissektor
Wählst du auf einer Kreislinie zwei Punkte aus und verbindest diese mit dem Kreismittelpunkt, dann erhältst du einen Ausschnitt des Kreises. Der Flächeninhalt des Kreisausschnitts (A) wird bestimmt durch die Größe des Mittelpunktswinkels α . Je größer der Winkel α ist, desto größer ist auch der Flächeninhalt des Kreisausschnitts
Zusammenhang zwischen dem Radius r und dem Kreisbogen b
♦Je größer der Radius r, desto größer die Bogenlänge b
♦zum doppelten Radius (2r) gehört die doppelte Bogenlänge (2b)
Zusammenhang zwischen dem Zentriwinkel ∝ und dem Kreisbogen b
♦Je größer der Zentriwinkel, desto größer die Bogenlänge
♦zum doppelten Zentriwinkel (2a) gehört die doppelte Bogenlänge (2b)
Merke: Zentriwinkel ist eine andere oder weitere Bezeichnung für den Mittelpunktswinkel an einem Kreisausschnitt
Formeln des Kreissektors
Flächeninhalt: A = r² * π * α : 360
Flächeninhalt: A = r * b : 2
Kreisbogen: b = d * π * α : 360
Umfang: U = 2 * r + b
Formeln für Umkehraufgaben
Flächeninhalt: A = r² * π * α : 360
⇒ α = A * 360 : (r² * π)
⇒ r = √[A * 360 : (α * π)]
Flächeninhalt: A = r * b : 2
⇒ r = 2 * A : b
⇒ b = 2 * A : r
Kreisbogen: b = d * π * α : 360
⇒ d = b * 360 : (π * α)
⇒ α = b * 360 : (d * π)
Umfang: U = 2 * r + b
⇒ r = (U – b) : 2
⇒ b = U – 2 * r
Grad- und Bogenmaß
♦Das Verhältnis zwischen Bogenlänge b und Radius r ist für jeden Mittelpunktswinkel konstant. Deshalb kann man mit diesem Verhältnis auch einen Winkel beschreiben. Für das Bogenmaß des Winkels gilt: arad= b/r
Merke: Das Bogenmaß ist immer eine reelle Zahl
Das Gradmaß arad/π = aDeg/180° → arad= aDeg/180° *π
Zusammenfassung
•kreis ist eine linie auf der jeder punkt den gleichen abstand hat zu einem festen punkt
•den festen punkt ist der Kreismittelpunkt M
•jeder punkt ist zum M gleich weit entfernt
•den abstand vom Mittelpunkt zum punkt ist der radius r
•die länge der geschlossenen kreislinie ist der Umfang U
•die geschlossene fläche heißt kreisfläche A
•eine zusätzliche gerade die durch den kreis führt heißt sekante
•eine teilstrecke nennt man sehne
•wenn eine sehne durch den mittelpunkt geht ist das der durchmesser d
•eine gerade in einem punkt berührt ist die targente
•die am kreis vorbei führt heißt passante
