Periodische Funktion
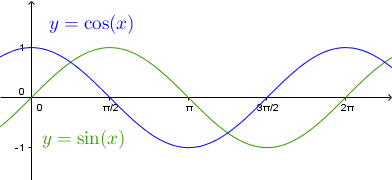
Die bekanntesten periodischen Funktionen sind die trigonometrischen Funktionen. Die Sinusfunktion und die Kosinusfunktion sind periodisch mit der Periode 2π.
Periode und Frequenz
Eine Funktion f(x) heißt periodisch mit Periode p, wenn f(x + p) = f(x) für alle x ∈ R gilt
(dabei sei p eine feste positive Zahl). Dies bedeutet, daß die vertikale Verschiebung um p die Funktion in sich überführt. Typische Beispiele periodischer Funktionen sind Sinus und Cosinus (beide mit Periode 2π).
Statt der Periode p betrachtet man oft den Kehrwert 1/p und nennt ihn die Frequenz (also die Häufigkeit der Wiederholung pro Zeiteinheit”): Ist f(t) eine Funktion mit der Periode 1/3 , gilt also f(t + 1/3 ) = f(t) für alle t, so ist die Frequenz 3: alles wiederholt sich 3 mal pro Zeiteinheit.
Die Schwingung f(t) = sin t schwingt pro 2π Sekunden einmal, sie hat also die Frequenz 1/2π [sec]-1 (und die Periode 2π). Die Standard-Maßeinheit für eine Zeitdauer ist die Sekunde, entsprechend ist die Standard-Maßeinheit für Frequenz die Anzahl pro Sekunde, also 1 sec ,auch Hz genannt (gesprochen: Hertz)
Unser Lernvideo zu : Periodische Funktion
Beispiel
Merke: Ist F die Frequenz (also die Anzahl der Wiederholungen pro Sekunde) und p die Periode (also die Dauer in Sekunden), so gilt
F= 1/p und p=1/F
Ist die x-Achse eine Zeitachse, so nennt man die Periode auch Periodendauer (und ihren Kehrwert Frequenz), ist die x-Achse dagegen eine räumliche Achse, so nennt man die Periode Wellenlänge (und den Kehrwert Wellenzahl).
Beispiel: Eine Woche hat 7 Tage, jeder Tag 86 400 Sekunden, also hat eine Woche 602 000 Sekunden, die Frequenz ist also 3, 3 · 10-6 Hz.
Streckungen und Stauchungen
Hat f die Periode p, so sind für beliebige Konstanten c > 0 und d die Funktionen df (ct) periodisch, und zwar mit Periode p/c . (Der Faktor d verändert die Amplitude!)
Funktion zeichnen und erkennen
f(x)= a*sin ( b*(x-c)+d → für Sinusfunktion
f(x)= a*cos( b*(x-c)+d →für Cosinusfunktion
f(x)= a*tan ( b*(x-c)+d →für Tangensfunktion
Bedeutung der Buchstaben
Die Amplitude a bewirkt eine Streckung
Der Faktor b bewirkt eine Änderung der Periodenlänge, welche durch die Formel p=2π/b berechnet wird.
Der Faktor c bewirkt eine Phasenverschiebung in x-Richtung. Wenn c>0 ist, dann verschiebt sich der Graph nach rechts, bei c<0 nach links
Der Faktor d bewirkt eine Verschiebung parallel der y-Achse um d. Das bedeutet, dass jedem Funktionswert die Zahl d dazu addiert wird.
Anhand dieser Merkmale kann man periodische Funktionen zeichnen und auch erkennen!
