Umfang eines Drachens
Hier findet ihr die Information zur Berechnung des Umfangs eines Drachens.
Dazu wiederholen wir, was ein Drachen ist und beginnen dann mit der Berechnung des Umfangs.
Zur Wiederholung:
Ein Drachen ist eine viereckige geometrische Figur. In der Mathematik wird der Drachen auch Deltoid genannt. Er besteht aus zwei Paaren gleich langer benachbarten Seiten und die Diagonalen der Figur sind senkrecht zu einander – treffen sich im rechten Winkel.
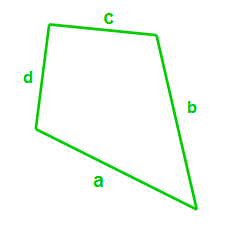
Abgebildet ist ein allgemeiner Drachen. Die Seiten sind aktuell mti a, b, c und d beschriftet. Da die nebeneinanderliegenden Setien, in diesem Fall Seite a und b und Seiten c und d gleich lang sind, können wir diese auch gleich benennen. Zusätzlich zeichen wie die Diagonalen e und f ein:
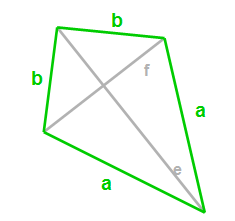
Nun haben wir einen allgemeinen Drachen mit allen dazugehörigen Bezeichnungen.
Lerntool zu Umfang eines Drachens
Unser Lernvideo zu : Umfang eines Drachens
Formel des Umfangs
Nun gehen wir Schritt für Schritt vor, um die Formel zur Berechnung des Umfangs zu lernen und vor allem zu verstehen.
Wie betrachten einen allgemeinen Drachen:
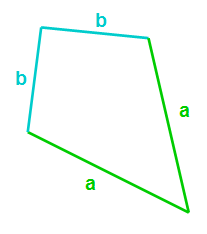
Ohne eine Formel zu kennen, könnten wir, um den Umfang zu erfahren, jede der Seiten miteinander addieren:
Umfang = a + a + b + b
Diese Rechnung können wir nach den Regeln der Mathematik zusammenfassen:
Umfang = 2•a + 2•b = 2 (a + b)
Somit haben wir die allgemeine Formel zu Berechnung des Umfangs eines Drachens ermittelt:
![]()
Es fällt auf, dass die Formel für die Berechnung des Umfangs eines Drachens die selbe ist, wie die eines Parallelograms oder Rechtecks. Wichtig ist hier daran zu denken, dass es in all den drei Figuren jeweils zwei gleichlange Seitenpaare gibt, jedoch sind die eines Drachens nicht parallel!
Beispiel 1
Wie berechnen nun den Umfang eines Drachens
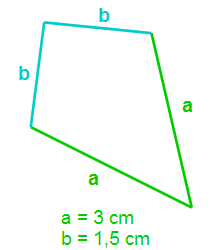
In unserem ersten Beispiel ist die Seite a = 3cm und die Seite b = 1,5 cm. Diese geben wir nun in unsere Formel ein und berechnen den Umfang des Drachen.
Gegeben: a = 3cm und b = 1,5cm
Gesucht: U
Formel: U = 2(a + b)
Einsetzen und berechnen: U = 2( 3cm + 1,5cm) = 2(4,5cm) =9cm
Antwort: Der Umfang des Drachens ist U = 9cm.
Beispiel 2
Als nächstes betrachten wir einen Drachen, von dem wir eine Seitenlänge und den Umfang kennen.
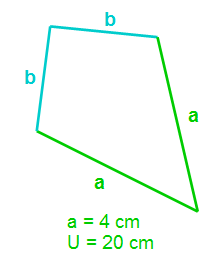
Bei dieserm Beispiel brauchen wir nicht den Umfang, sondern die uns unbekannte Seitenlänge der Seite b.
Dazu müssen wir zunächst unsere Formel nach b umstellen:
U = 2(a + b) | :2
U:2 = a + b | -a
U:2 – a = b
Nun haben wir die Formel nach b umgestellt und können nun unsere Rechnung fortführen:
Gegeben: U = 20cm und a = 4 cm
Gesucht: b
Formel: b = U:2 – a
Einsetzen und berechnen: b = 20cm :2 – 4cm = 10cm – 4cm = 6cm
Antwort: Unsere unbekannte Seitnlänge b ist 6cm lang.
