Umfang eines Parallelogramms
Wenn du den Umfang eines Parallelogramms wissen möchtest, findest du hier den Weg dorthin.
Um ein Parallelogramm zu berechnen, müssen wir wissen, was ein Parallelogramm als geometrische Figur ausmacht.
Wiederholung:
Ein Parallelogramm ist ein Viereck mit vier Ecken und vier Seiten. Die gegenüberliegenden Winkel sind gleich groß und alle Winkel ergeben insgesamt 360°. Auch die gegenüberliegenden Seiten eines Parallelogramms sind gleich lang.
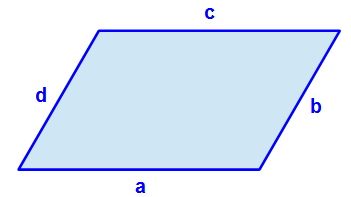
Abgebildet ist ein allgemeines Parallelogramm. Die gegenüberliegende Winkel sind gleich groß. Ebenso sind auch die gegenüberliegende Seiten gleich groß. Die Seiten, die zur Berechnung des Umfangs ausschlaggebend sind, sind hier mit a, b, c und d beschriftet. Da die gegenüberleigenden Seiten identisch sind, können wir dieses in der Beschriftung berücksichtigen.
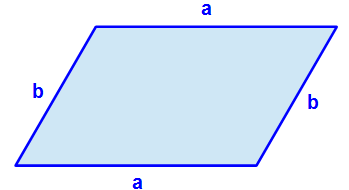
Nun ist unser Parallelogramm korrekt beschriftet. Wir nehmen zunächst immer als Seitenbezeichnung die Variablen a und b. Dies ist aber nicht in Stein gemeißelt, einfach nur üblich.
Lerntool zu Umfang eines Parallelogramms
Unser Lernvideo zu : Umfang eines Parallelogramms
Formel des Umfangs
Auch hier wollen wir step by step uns zur Formel der Umfangsberechnung vorarbeiten.
Wir nehmen uns zunächst ein Beispiel und dann verallgemeinern wir dieses.
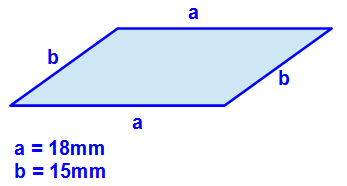
In diesem Beispiel sehen wir ein Parallelogramm, welches die Seitenlängen a = 18mm und b = 15mm hat. Da die Maßeinheiten identisch sind, brauchen wir diese nicht angleichen. Um nun den Umfang zu berechnen, gehen wir ganz direkt vor, indem wir alle Seitenlängen addieren.
U = 18mm + 15mm + 18mm + 15mm = 2•18mm + 2•15mm = 66mm
Allgemein können wir das wie folgt ausdrücken:
U = a + b + a + b = a + a + b + b = 2•a + 2•b = 2(a + b)
Somit haben wir die Formel für den Umfang eines Parallelogramms ermittelt:
![]()
Spätestens an der Formel erkennen wir, dass wir hier die gleiche Rechnung haben wie beim Umfang eines Rechtecks. Dies liegt daran, dass bei beiden Figuren die gegenüberliegenden Seiten gleich lang sind. Der Unterschied der beiden ist, dass in einem Rechteck die Winkel immer 90° betragen. Dies muss in einem Parallelogramm nicht so sein. Dort sind nur die gegenüberliegenden Winkel identisch groß.
Zum Verständnis: Jedes Rechteck ist ein Parallelogramm, aber nicht jedes Parallelogramm ist ein Rechteck.
Beispiel 1
Wir berechnen nun den Umfang eines Parallelogramms
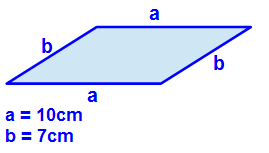
Die Seitenlängen sollen a = 10cm und b = 7 cm sein und der Umfang soll ermittelt werden. Da die Maßeinheiten bereits in der selben Einheit sind, brauchen wir diese nicht angleichen.
Gegeben: a = 10cm und b = 7cm
Gesucht: U
Formel: U = 2a + 2b
Einsetzen und berechnen: U = 2•10cm + 2•7cm = 20cm + 14 cm = 34cm
Antwort: Der Umfang des Parallelogramms beträgt U = 34cm.
Beispiel 2
Wir betrachten ein Parallelogramm, in dem uns nur eine Seite und der Umfang gegeben ist. Wir möchten die fehlende Seite ermitteln.
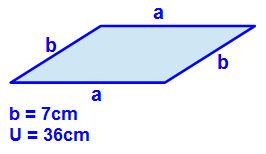
Die Seite b = 7cm und der Umfang U = 36 cm. Da die Maßeinheiten in cm angegeben sind, brauchen wir diese nicht umzurechnen, sondern können uns direkt an die Ermittlung der Seitenlänge a machen. Dazu stellen wir zunächst unsere Formel nach a um:
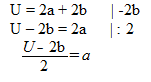
Gegeben: b = 7cm, U = 36cm
Gesucht: a
Einsetzen und berechnen:
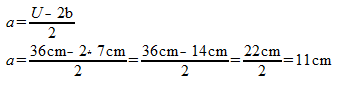
Antwort: Die Seitenlänge a beträgt 11cm.
