Umfang eines Quadrats
Hier erklären wir dir, wie man den Umfang eines Quadrats berechnet.
Um den Umfang eines Quadrats berechnen zu können, muss man natürlich wissen, was ein Quadrat ist.
Zur Wiederholung
Ein Quadrat ist ein Viereck mit vier Ecken und vier Seiten. Die Ecken haben jeweils einen Winkel von 90°, die Winkel ergeben isngesamt 360° und alle Seiten sind gleich lang.
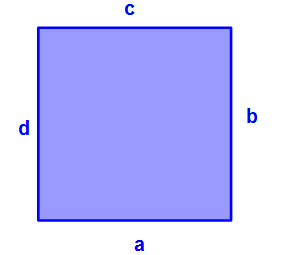
In der obigen Abbildung sehen wir ein blaues Quadrat. Zur Berechnung des Umfangs beachten wir hier nur den dunkelblauen Rand. Die Seiten sind zunächst beschriftet mit a, b, c und d. Da alle Seiten in einem Quadrat gleich lang sind, ändern wir die Seitenbezeichnungen dementsprechend.
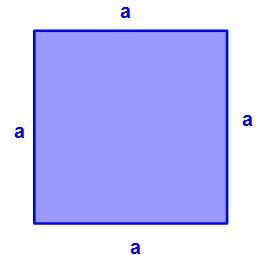
Nun ist das allgemeine Quadrat korrekt beschriftet.
In der Mathematik nutzt man als Seitenbezeichnung zumeist den Buchstaben a. Dies ist aber nicht bindend, man könnte auch b, c oder f nehmen.
Lerntool zu Umfang eines Quadrats
Unser Lernvideo zu : Umfang eines Quadrats
Die Formel des Umfangs
Um die allgemeine Formel zu ermitteln, gehen wir nun Schritt für Schritt an einem Beispiel vor:
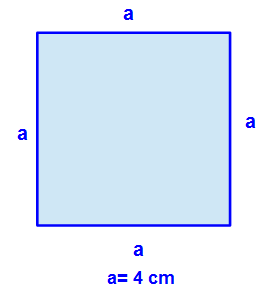
Wir haben ein Quadrat mit vier gleich langen Seiten. Die Seitenlänge ist 4 cm.
Ohne eine Formel zu wissen, kann man den Umfang dieses Quadrats berechnen, in dem mal alle vier Seitenlängen miteinander addiert: 4cm + 4cm + 4cm + 4cm = 16cm
Allgemein ausgedrückt haben wir gerechnet: a + a + a + a = 4a
Wir haben nun herausgefunden, dass der Umfang eines Quadrats wie folgt lautet:
![]()
Diese Formel ist so anwendbar und du kannst deine bekannten Größen eingeben und ggf. die Gleichung auch umstellen.
Beispiel 1:
Wir möchten den Umfang eines Quadrats mit der Seitenlänge 3m berechnen.
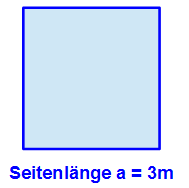
Die Formel lautet: U = 4a
Gegegeben: a = 3m
Gesucht: U
Einsetzen der bekannten Größen: U = 4 • 3m
Berechnen: U = 4 • 3m = 12m
Antwort: Der Umfang ist U = 12m.
Beispiel 2:
Nun ist die Aufgabe ein wenig anders. Wir kennen bereits den Umfang und möchten die Seitenlänge wissen:

Nun haben wir eine etwas andere Ausgangssituation. Wir kennen nicht die Seitenlänge, sondern bereits den Umfang und möchten aber die Seitenlänge berechnen. Hier machen wir uns zu Nutze, dass unsere Formel eine Gleichung ist.
Formel: U = 4a
Gegeben: U = 20m
Gesucht: a
Einsetzen der bekannten Großen: 20m = 4a
Berechnen:
20m = 4•a | :4 (wir teilen durch 4 auf beiden Seiten der Gleichung)
5m = a
Antwort: Die gesuchte Seitenlänge ist a = 5m.
Wir haben ausgenutzt, dass wir eine Gleichung als Formel haben und können somit mit beiden Ausgangssituationen rechnen und zu einem Ergebnis gelangen.
