Umfangswinkelsatz
Der Umfangwinkelsatz oder Peripheriewinkelsatz sind zwei Namen für dieselbe Aussage. Manchmal wird ein Umfangswinkel auch als Randwinkel bezeichnet. Veränderungen im Vokabular ist allerdings keine Veränderung in der mathematischen Aussage.
Die Aussage wird folgendermaßen beschrieben: Für alle Dreiecke ABC, bei denen C auf einem festen Kreisbogen (der Peripherie) über der festen Sehne AB liegt, ist der Winkel im Punkt C immer gleich groß! (Dabei liegt C immer auf der selben Seite der Sehne.)
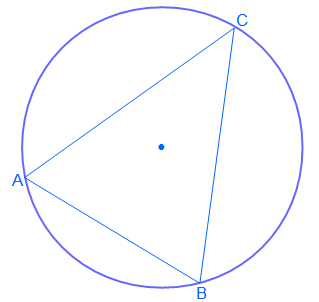
Wir betrachten die Aussage des Satzes nun genauer.
Unser Lernvideo zu : Umfangswinkelsatz
Erklärung
Die Aussage bedeutet, dass wir einen beliebigen Kreis haben und darin eine Sehne zeichnen, die die Punkte A und B hat. Diese Punkte liegen beide auf dem Kreis und sind fest. Nun können wir für ein Dreieck einen weiteren Punkt auf der Kreislinie (der Peripherie) zeichnen. Der Umfangswinkelsatz sagt nun aus, dass jeder Punkt auf auf der jeweiligen Seite der Sehne immer die selbe Winkelgröße hat.
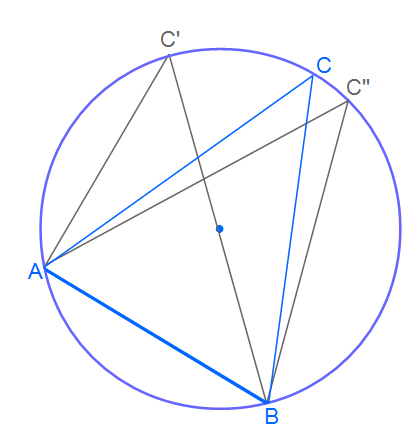
Wir sehen in der Abbildung einen beliebigen Kreis mit einem Mittelpunkt. Am Kreis sind verschiedene Punkte. Zunächst die Punkte A und B, die eine Strecke bilden, die wir nun Sehne nennen. Diese ist dick und blau dargestellt. Diese Sehne ist fest, sie bewegt sich nicht. Desweiteren sehen wir drei Punkte über dieser Sehne: C, C‘ und C“. Diese Punkt liegen jeweils auf der Peripherie bzw. auf dem Kreisbogen. Egal wo wir den Punkt C setzen, solange er auf der selben Seite der Sehne ist und auf dem Kreisbogen liegt, hat er immer die selbe Winkelgröße.
Der Kreisbogen an der Sehne, heißt auch Fasskreisbogen. An jeder Sehne gibt es je zwei Fasskreisbögen. In unserer Abbildung liegen auf dem kleineren Fasskreisbogen keine Punkte.
Beweis
Bisher haben wir uns die Aussage genau angesehen, Nun wollen wir diese auch beweisen. Als Formel geschreiben, können wir die Aussage wie folgt notieren: γ = γ‘
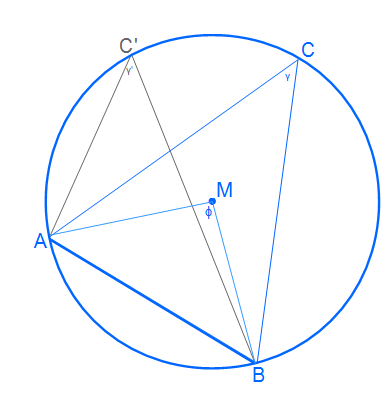
Um den Umfangswinkelsatz zu beweisen, nehmen wir uns die Abbildung zur Hilfe. Wir haben bereits bewiesen, dass der Mittelwinkel immer doppelt so groß ist wie der Umfangswinkel. Dies kannst du nochmal beim Thema Kreiswinkelsatz nachlesen. Diesen Beweis übertragen wir nun auf die neue Situation.
Da jeder Umfangswinkel halb so groß ist wie der Mittelpunktswinkel, müssen diese untereinander gleich groß sein. Also ist γ = γ‘, da beide auf dem selben Fasskreisbogen über der Sehne AB liegen und somit den selben Mittelpunktswinkel haben.
