Umwandeln von Dezimalzahlen in Brüche
Nun schauen wir uns an, wie wir Dezimalbrüche in einfache Brüche wandeln können. Dies wird des öfteren benötigt, weil oft gemischte Aufgaben mit Brüchen und Dezimalbrüchen gestellt werden.
Dieses ist nicht schwer, man muss sich dazu nur die Stellenwerttafel der Dezimalzahlen zurück ins Gedächtnis rufen, da wir die Bezeichnung der Nachkommastellen benötigen.
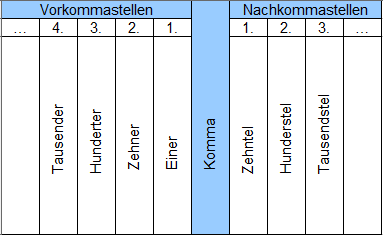
An der Stellenwerttafel sehen wir, wie die Benennungen der Nachkommastellen sind. Es gibt Zehntel, Hunderstel, Tausendstel usw. Dies wenden wir beim Umwandeln an.
Unser Lernvideo zu : Umwandeln von Dezimalzahlen in Brüche
Umwandlung einer Dezimalzahl in einen Bruch
Methode 1: Nachkommastellen zählen
Wenn uns eine Dezimalzahl gegeben ist und diese wollen wir in einen Bruch umwandeln. Dann sehen wir uns zuerst an, wie viele Nachkommastellen hat unsere Dezimalzahl. Dann setzen wir die Nachkommazahl in den Zäher und der Stellenwert der Zahl kommt in den Nenner des Bruches. Somit haben wir einen Bruch generiert. Als nächstes überprüfen wir, ob wir diesen noch kürzen können und dann sind wir auch schon fertig.
Wir betrachten dieses in Beispielen:
Beispiel 1:
0,5 soll in einen Bruch gewandelt werden
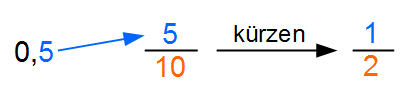
Die 5 kommt in den Zähler des Bruches. Da es nur eine Stelle nach dem Komma ist, handelt es sich um Zehntel. Dies notieren wir im Nenner. Dann kürzen wir und erhalten unseren Bruch.
Beispiel 2:
0,25 soll in einen Bruch gewandelt werden
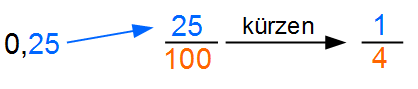
Die Nachkommazahlen werden in den Zähler des Bruches gesetzt. Da es sich bei zwei Stellen um Hunderstel handel, setzen wir dieses in den Nenner. Nach dem Kürzen erhalten wir unseren fertigen Bruch.
Beispiel 3:
1,025 soll in einen Bruch gewandelt werden
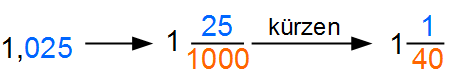
Nun haben wir den Unterschied, dass auch vor dem Komma eine Zahl steht. Dieses sind Ganze. Die nehmen wir als solche auch weiter mit. Wieder kommt die 25 in den Zähler. Die Null vor der 25 lassen wir weg. In den Nenner kommt die 1000, da wir drei Nachkommastellen haben. Nach dem wir gekürzt haben, erhalten wir einen gemischten Bruch.
An den Beispielen ist zu erkennen, dass es sich immer um die Anzahl der Nachkommastellen handelt, um ermitteln zu können, welchen Bruch wir haben. Nicht außer acht zu lassen, ist es zu kürzen, da man somit den Bruh und auch spätere Rechnungen viel einfacher macht. Wenn ihr euch das Kürzen nochmal ansehen wollt, könnt ihr dieses gerne auch auf dieser Homepage.
Neben der ersten Methode – die Nachkommastellen zu zählen, gibt es noch zwei andere Möglichkeiten, um Dezimalzahlen in Brüche zu umzurechnen.
Methode 2: Periodenlänge zählen
Insbesondere für die periodischen Dezimalzahlen eignet sich diese Methode. Zuerst zählen wir die Stellen der Periode. Wir beantworten also die Frage, wie viele Stellen unter einem Periodenstrich stehen.
- Nenner = so viele Neunen, wie die Periode Stellen hat
- Zähler = die Periode selbst
Was vielleicht in der Theorie etwas kompliziert klingt, stellt sich in der Praxis als kinderleicht heraus. Hier eines der deutlichsten Beispiele, wie man die Periodenlänge zählen kann.
Beispiel
Was tun bei gemischtperiodischen Dezimalzahlen?
Aber auch hier gibt es eine Sonderform, wenn wir es mit gemischtperiodischen Dezimalzahlen zu tun haben. Hier sollte man zunächst die Zahl mit einer Potenz von 10 multiplizieren, denn danach entsteht eine rein periodische Dezimalzahl. Erst dann können wir die Zahl, wie oben gesehen, ganz einfach in den Bruch umwandeln. Das wird an dem folgenden Beispiel am deutlichsten.
Methode 3: Auswendiglernen
Zugegeben, diese Methode klingt doch recht stupide, kann aber helfen, recht komplexe Rechenaufgaben in ein paar Augenblicken zu bewältigen. So ist es hilfreich, die geläufigsten Brüche und Dezimalzahlen einfach auswendig zu lernen, um sich selbst das mathematische Leben zu erleichtern.
Der Bruch 1/2 entspricht der Dezimalzahl 0,5. Der Bruch 1/3 entspricht der periodischen Dezimalzahl 0,3 (Periode drei). Ohne mathematische Detailkenntnisse lassen sich auf diese Weise mit gerade einmal 12 auswendig gelernten Brüchen und dazugehörigen Dezimalzahlen jede Menge Rechenaufgaben in Sekundenschnelle korrekt ausrechnen. Warum sollte man sich dann noch lange quälen, wenn die Lernarbeit in ein paar Minuten erledigt ist?

Alternativ dazu kann man Brüche in Dezimalzahlen umwandeln, indem man einfach den Nenner auf 10, 100 oder 1000 erweitert. Doch machen wir damit wieder ein neues Thema auf. Nun ist es an der Aufgabe, die oben genannten Methoden erst einmal zu trainieren
