Varianz berechnen
Die Varianz ist ein Maß für die Abweichung einer Zufallsvariablen X von ihrem Erwartungswert μ in der Stochastik. Sie beschreibt die mittlere quadratische Abweichung der Werte der Zufallsvariablen zum Erwartungswert.
Problemstellung
Wir wissen bereits, dass sich die Wahrscheinlichkeitsverteilung einer Zufallsvariablen entweder
- durch die Verteilungsfunktion oder
- die Wahrscheinlichkeitsfunktion(bei diskreten Zufallsvariablen)
bzw. die Dichtefunktion (bei stetigen Zufallsvariablen)
vollständig beschreiben lässt.
Welche Aussage trifft die Varianz?
- Der Varianz ist ein „Streuungsparameter“. Unter diesem Begriff werden alle Maßzahlen zusammengefasst, die eine Aussage über die Streuung einer Verteilung machen. Die Varianz beschreibt die erwartete quadratische Abweichung der Zufallsvariablen von ihrem Erwartungswert.
- Nachteil der Varianz ist, dass sie aufgrund der Quadrierung eine andere Einheit als die beobachteten Messwerte besitzt. Auf den ersten Blick können somit keine konkreten Aussagen über die Streuungsbreite abgeleitet werden. In der Praxis wird daher häufig die Standartabweichung, die sich aus Quadratwurzel der Varianz ergibt, herangezogen.
Unser Lernvideo zu : Varianz berechnen
Die Formel für die Varianz ist
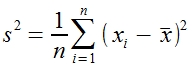
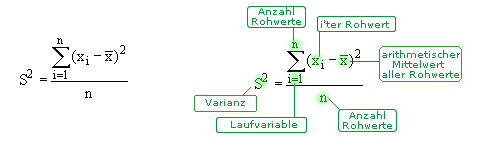
Aus der Varianz kann man nun die Standardabweichung berechnen. Die Standardabweichung ist nämlich die positive Quadratwurzel aus der Varianz.
Varianz berechnen: Beispiel
Man gehe beispielsweise von folgender geordneter Urliste aus: {2,4,5,6,8,9,14,16}. Erst einmal muss man das arithmetische Mittel von den gegebenen Werten bilden. Dies geht, in dem man alle Werte aufsummiert und dann durch die Anzahl teilt: (2 + 4 + 5 + 6 + 8 + 9 +14 +16)/8 = 8
Nun kann die Varianz berechnet werden: ((2-8)2 + (4-8)2 + (5-8)2 + (6-8)2 + (8-8)2 + (9-8)2 + (14-8)2 + (16-8)2) /8 = 20,75
Die Standardabweichung wäre in diesem Fall √(20,75) ≈ 4,555
Merke Dir
- Die Standardabweichung ist entweder eine positive Zahl oder Null. Sie ist niemals negativ. Die Standardabweichung ist Null, wenn alle Werte gleich sind. Da sie von der Varianz abgeleitet ist, bedeutet eine größere Standardabweichung auch eine höhere Varianz und umgekehrt.
- Die Standardabweichung kann sehr schnell steigen, wenn Werte, die weiter von den übrigen entfernt sind, mit in die Berechnung einbezogen werden.
- Die Einheit der Standardabweichung und die Einheit der Messwerte sind gleich.
