Vektorrechnung: Addition, Subraktion, Skalarprodukt
Wir befassen uns mit den Rechenarten der Vektoren. Dabei unterscheiden wir zwischen 3 Grundrechenarten.
Grundrechenarten der Vektorrechnung
- Addition
- Subtraktion
- Skalarprodukt
Zur jeder Grundrechenart werden wir jeweils einen Beispiel durchgehen, damit es verständlich wird.
Vektoraddition
Voraussetzung für die Addition von Vektoren:
- Vektoren lassen sich nur dann addieren, wenn sie gleicher Dimension und gleicher Art sind.
- Vektoren lassen sich nicht addieren, wenn sie zwar gleicher Art aber nicht gleicher Dimension sind oder andersrum
Um es euch zur verdeutlichen, rechnen wir gemeinsam einen Beispiel durch.
DieFormel für die Vektoraddition ist
![]()
Wir berechnen jetzt ein Beispiel mit Hilfe der Formel
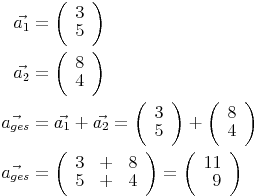
Vektorsubtraktion
Voraussetzung für die Subtraktion von Vektoren
- Vektoren lassen sich nur dann subtrahieren, wenn sie gleicher Dimension und gleicher Art sind.
- Vektoren lassen sich nicht subtrahieren, wenn sie zwar gleicher Art aber nicht gleicher Dimension sind oder umgekehrt
Formel Vektorsubtraktion:
![]()
Beispielaufgabe
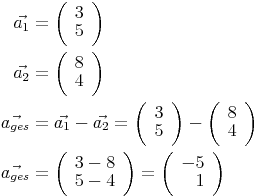
Skalarprodukt
Das Skalarprodukt ist nichts anderes als die Multiplikation zweier Vektoren miteinander.
Die Grundformel für die Multiplikation ist:
![]()
Wir berechnen dazu jetzt den folgenden Beispiel
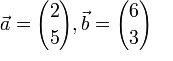
wir setzen ein:
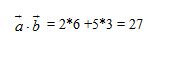
Also ist die Zahl 27 unser Skalarprodukt!
