Hessesche Normalform
Hessesche Normalform einer Geraden (nur im R2 möglich!)
Bedeutung
- n: Normalenvektor .
Der Normalenvektor ist ein Vektor, der mit der Gerade einen rechten Winkel bildet.
- N : normierter Normalenvektor (oder Normaleneinheitsvektor)
- Es gilt: n⃗0=n⃗|n|
- |n|: Länge des Normalenvektors
- a : Aufpunkt (oder Stützvektor)
Besonderheit
Eine Gerade lässt sich lediglich im R2 in Normalenform darstellen, weil es im R3 keinen eindeutigen Normalenvektor gibt!
Hessesche Normalform einer Ebene
Bedeutung
- n: Normalenvektor
Der Normalenvektor ist ein Vektor, der senkrecht auf der Ebene steht. - n0: normierter Normalenvektor (oder Normaleneinheitsvektor)
Es gilt:n 0=n|n| - |n|: Länge des Normalenvektors
- a: Aufpunkt (oder Stützvektor)
Unser Lernvideo zu : Hessesche Normalform
Bedeutung der Hesseschen Normalform
♦Die Hessesche Normalform spielt vor allem bei der Berechnung des Abstands Punkt-Ebene eine Rolle.
♦Wenn man einen beliebigen Punkt in die Hessesche Normalform einsetzt, erhält man als Ergebnis den Abstand dieses Punktes von der Ebene.
Beispiel
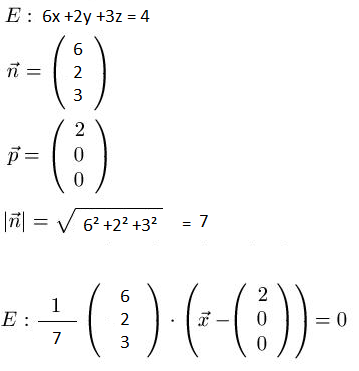
Beispiel 2