Flächenschwerpunkt im Viereck
In jedem Viereck gibt es einen bestimmten Punkt, an dem man das Viereck balancieren kann. Diesen Punkt nennt man Schwerpunkt. Genau an diesem Punkt ist das Gewicht komplett ausgeglichen.
Wir können unter drei verschiedenen Schwerpunkten unterscheiden:
– Flächenschwerpunkt: Die Masse ist gleichmäßig auf der Fläche verteilt.
– Eckenschwerpunkt: Die Masse sitzt in den Ecken und ist gleich verteilt.
– Kantenschwerpunkt: Die Masse ist gleichmäßig auf die Seiten verteilt.
Bei einem Dreieck stimmt der Flächenschwerpunkt und der Eckschwerpunkt überein. Der Kantenschwerpunkt wird nur selten betrachtet, stimmt aber nicht mit den beiden anderen überein.
In einem Viereck können die Schwerpunkte gleich sein, müssen es allerdings nicht. Wir betrachten zunächst alle konvexen ebenen Vierecke.
Unser Lernvideo zu : Flächenschwerpunkt im Viereck
Schwerpunkt im Parallelogramm
In jedem Parallelogramm (auch Quadrat, Rechteck…) fällt der Eckenschwerpunkt mit dem Flächenschwerpunkt zusammen. Er liegt genau auf dem Schnittpunkt der beiden Diagonalen.
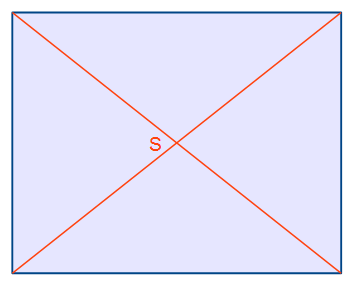
In der Abbildung sehen wir ein Rechteck, was auch ein Parallelogramm ist. Die beiden Diagonalen treffen sich in einem Punkt. Dieser Punkt S ist sowohl der Flächenschwerpunkt als auch der Eckschwerpunkt des Parallelogramms.
Flächenschwerpunkt
Wenn sich die Masse eines Vierecks auf die Fläche verteilt, suchen wir den Flächenschwerpunkt. Dieser lässt sich ermitteln, in dem man das Viereck zunächst mit einer Diagonalen in zwei Dreiecke teilt und von diesen Dreiecken die Schwerpunkte ermittelt und mit einer Linie verbindet. Als nächsten Schritt teilt man dasselbe Viereck mit der zweiten Diagonle in zwei andere Dreiecke und ermittelt auch davon die Schwerpunkte. Die Verbindungslinie davon schneidet die erste und der Schnittpunkt der beiden Schwerpunktlinien ist der Schwerpunkt des Vierecks.
Nun schauen wir uns Schritt für Schritt das Ermitteln eines Flächenschwerpunkts im Viereck an.
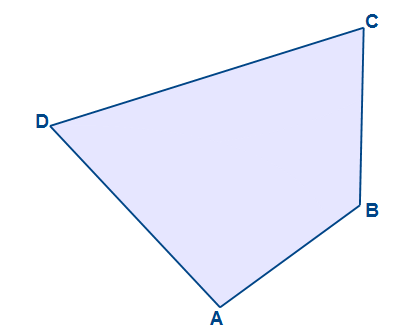
Wir betrachten ein konvexes ebenes allgemeines Dreieck. Die Eckpunkte sind ABCD. Da wir kein Parallelogramm haben, ist der Schnittpunkt der Diagonalen nicht der Flächenschwerpunkt des Vierecks.
Daher zeichnen wir zunächst eine Diagonale ein.
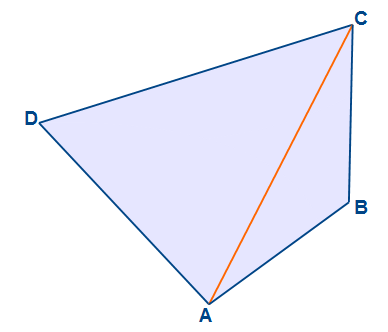
Die erste Diagonale reicht vom Eckpunkt A zum Eckpunkt C. Nun entstehen zwei Dreiecke: ABC und ACD. Von beiden Dreieck werden nun die Schwerpunkte ermittelt. Dieses geschieht in dem man die Seitenhalbierenden der drei Seiten einzeichnet. Der Schnittpunkt der Drei Seitenhalbierenden ist der Schwerpunkt. Ein Seitenhalbierende reicht vom MIttelpunkt einer Seite zum gegenüberliegenden Punkt. Mehr zur Konstruktion findet ihr auf unserer Homepage unter dem Punkt Seitenhalbierenden.
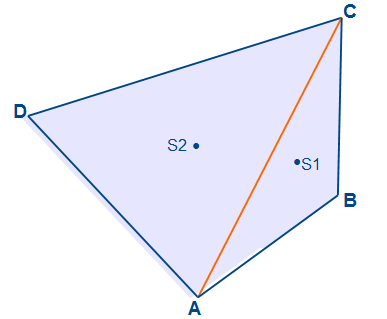
In der obigen Abbildung sehen wir die beiden ermittelten Schwerpunkte der Dreiecke ABC und ACD.
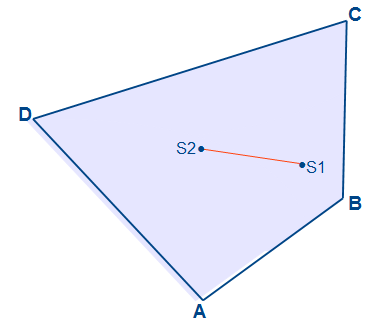
Wir verbinden die beiden Schwerpunkte und erhalten eine Schwerpunktlinie. Der Schwerpunkt des Vierecks liegt auf dieser Linie.
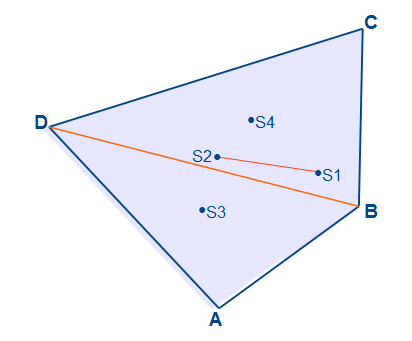
Im nächsten Schritt wird die andere Diagonale eingezeichnet und wir erhalten die Dreieecke ABD und BCD. Auch von diesen beiden Dreiecken ermitteln wir durch die Seitenhalbierenden die Schwerpunkte S3 und S4.
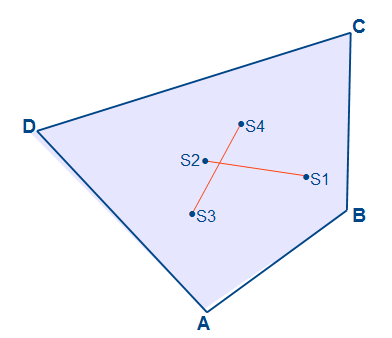
Wir verbinden die beiden Schnittpunkte. Nun scheidet die Schwerpunktlinie S1S2 die Schwerpunktlinie S3S4. Der Schnittpunkt der beiden Schwerpunktlinien ist der Flächenschwerpunkt des Vierecks.
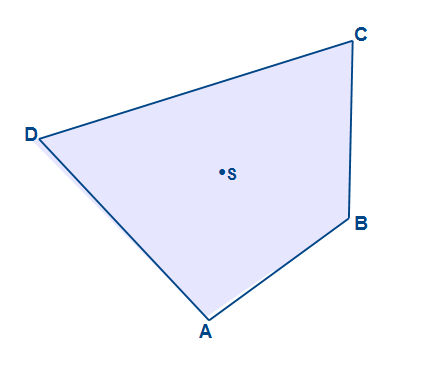
Durch die einzelnen Schritte konnten wir den Flächenschwerpunkt des Vierecks ermitteln. Dieser Vorgang ist für jedes konvexe ebene Viereck anwendbar.
