Kantenschwerpunkt im Viereck
In jedem Viereck gibt es einen bestimmten Punkt, an dem man das Viereck balancieren kann. Diesen Punkt nennt man Schwerpunkt. Genau an diesem Punkt ist das Gewicht komplett ausgeglichen.
Wir können unter drei verschiedenen Schwerpunkten unterscheiden:
– Flächenschwerpunkt: Die Masse ist gleichmäßig auf der Fläche verteilt.
– Eckenschwerpunkt: Die Masse sitzt in den Ecken und ist gleich verteilt.
– Kantenschwerpunkt: Die Masse ist gleichmäßig auf die Seiten verteilt.
Bei einem Dreieck stimmt der Flächenschwerpunkt und der Eckschwerpunkt überein. Der Kantenschwerpunkt wird nur selten betrachtet, stimmt aber nicht mit den beiden anderen überein.
In einem Viereck können die Schwerpunkte gleich sein, müssen es allerdings nicht. Wir betrachten zunächst alle konvexen ebenen Vierecke.
Unser Lernvideo zu : Kantenschwerpunkt im Viereck
Kantenschwerpunkt
Der Kantenschwerpunkt ist anders als die beiden anderen Schwerpunkte nur selten zu betrachten, trotzdem wollen wir ihn hier behandeln.
Beim Kantenschwerpunkt gehen wir davon aus, dass die gesammte Masse des Vierecks nur auf die Kanten verteilt ist z.B. ein Viereck aus Draht oder Eisen oder ähnliches. Der Schwerpunkt dieses Vierecks liegt nicht bei den Schwerpunkten der Fläche oder der Ecken. Auch in einem Parallelogramm muss der Schwerpunkt nicht auf dem selben Punkt liegen wie der Flächen- oder der Eckenschwerpunkt.
Wir betrachten nun wie wir den Kantenschwerpunkt ermitteln können ohne Vektoren nutzen zu können. Vektoren lernt ihr erst in einem späteren Zeitpunkt kennen.
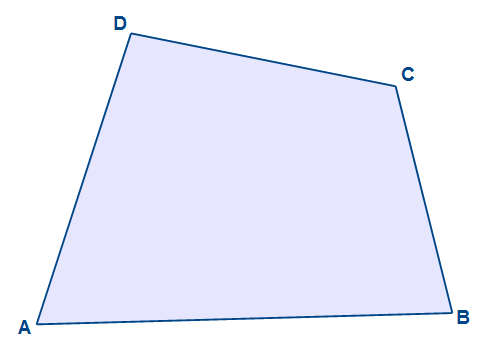
Wir gehen von einem allgemeinem konvexen Viereck aus. Dieses wird zunäcst wie bereits bei den anderen Schwerpunkten in ein Dreieck unterteilt.
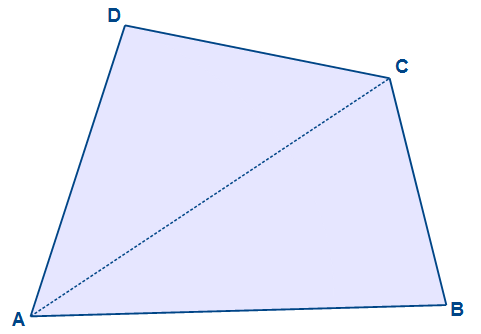
Wir zeichnen eine Diagonale von A zu C, somit teilen wir das Viereck in zwei Dreiecke. Das Dreieck ABC und das Dreieck ACD. Nun wird zunächst von jedem dieser beiden Dreiecke der Kantenschwerpunkt ermittelt.
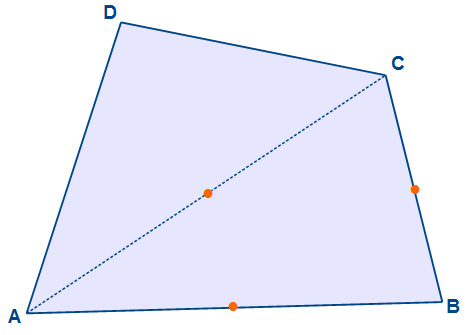
Dazu markieren wir die Mitte der einzelnen Strecken. Also die Mitte von AB, die Mitte von BC und die Mitte von CA. Dieses können wir entweder abmessen mit einem Lineal oder wir konstruieren die Mitte mit dem Zirkel. Dieses haben wir bereits bei dem Flächenschwerpunkt durchgeführt, so dass ihr euch dieses gerne nachschauen könnt. Kurz beschrieben: man zieht je einen Kreis um die beiden Eckpunkte mit dem selben Radius. Dann verbindet man die Schnittpunkte der Kreise und dort wo die Hilflinie, die Kante schneidet ist der Mittelpunkt der betrachteten Strecke.
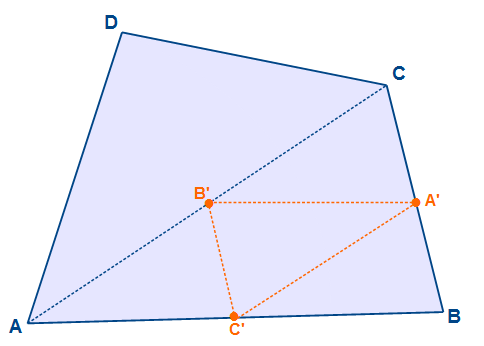
Diese Mittelpunkte verbinden wir mit Hilflinien und benennen die Eckpunkte mit A‘, B‘ und C‘. Dieses orange Dreieck ist das sogenannte Innendreieck des Dreiecks ABC. Im nächsten Schritt werden die einzelnen Winkelhalbierenden des Innendreiecks eingezeichnet.
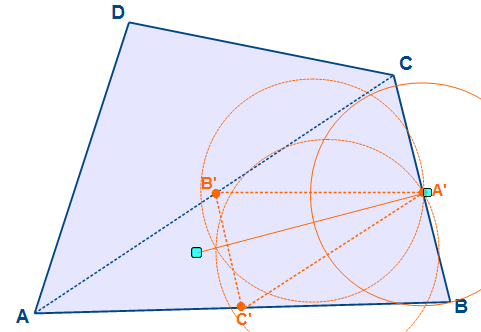
In der obigen Abbildung seht ihr, wie man zeichnerisch die Winkelhalbierende ermittelt. Zunächst zieht man einen Kreis um den Punkt A‘. Dieser schneidet die beiden Schenkel A’C‘ und A’B‘. Bei den Schnittpunkten ziehen wir den gleichen Kreis. Die Schnittpunkte der beiden letzten Kreise werden nun verbunden und dies ergibt die Winkelhalbierende.
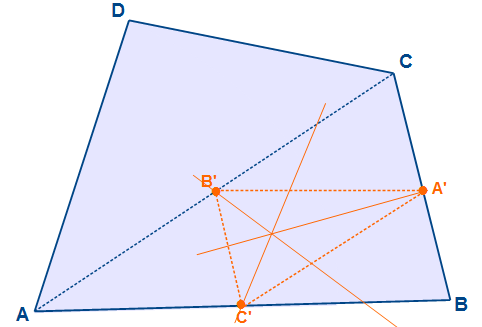
Diesen Vorgang wiederholen wir für die beiden anderen Winkel in B‘ und C‘. Alle drei Winkelhalbierende treffen sich in einem Punkt. Dieses ist der Kantenschwerpunkt des Ausgangsdreiecks ABC.
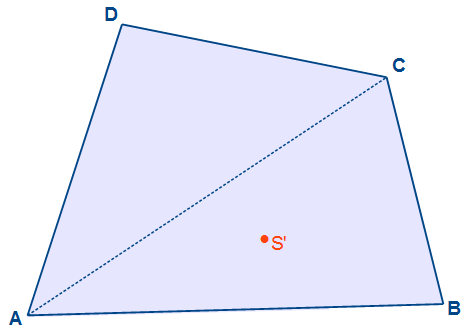
Nun haben wir den ersten Kantenschwerpunkt ermittelt. Dieses müssen wir nun wiederholen, um auch den Kantenschwerpunkt des Dreiecks ACD zu erhalten.
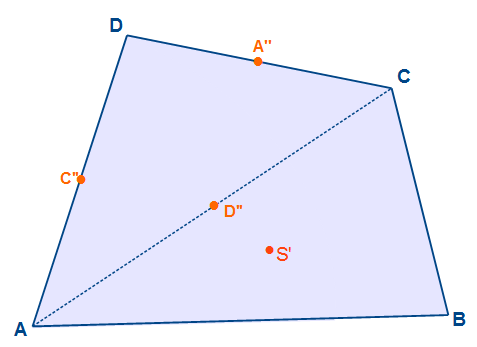
Genau wie beim ersten Dreieck werden auch bei dem Dreieck ACD zunächst die Mittelunkte der Seiten ermittelt und verbunden. Danach werden die drei Winkelhalbierende gezeichnet. Der Schnittpunkt ergibt den Kantenschwerpunkt des Dreiecks ACD.
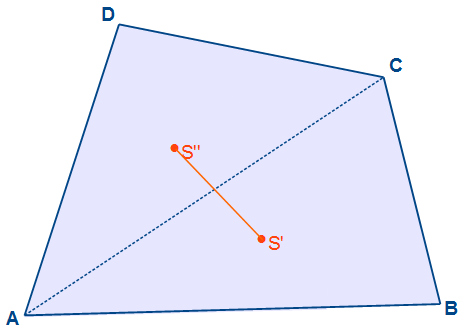
Wir verbinden die beiden Kantenschwerpunkte. Auf dieser Linie liegt der Kantenschwerpunkt des Vierecks ABCD.
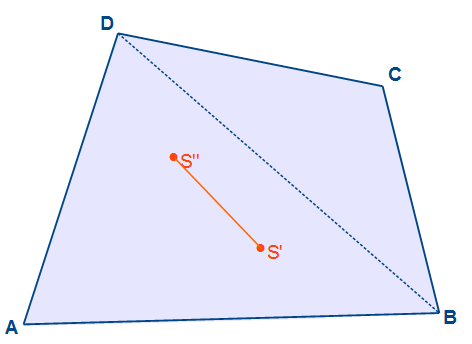
Im nächsten Schritt zeichnen wir die zweite Diagonale des Vierecks von B zu D. Nun haben wir zwei neue Dreiecke: ABD und BCD. Auch von diesen beiden Dreiecken werden wie oben beschreiben die Kantenschwerpunkte ermittelt.
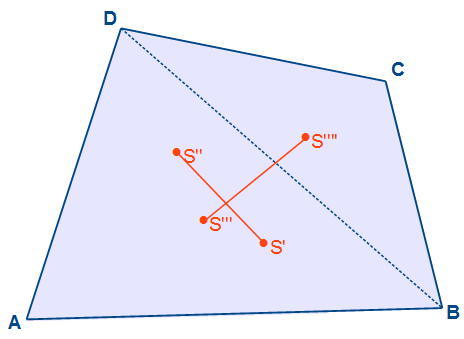
Wenn wir von beiden Dreiecken die Kantenschwerpunkte ermittelt haben, werden auch diese verbunden. Der Schnittpunkt der beiden Kantenschwerpunktslinien schneiden sich in genau einem Punkt. Dieser Punkt ist nun der Kantenschwerpunkt des Vierecks ABCD.
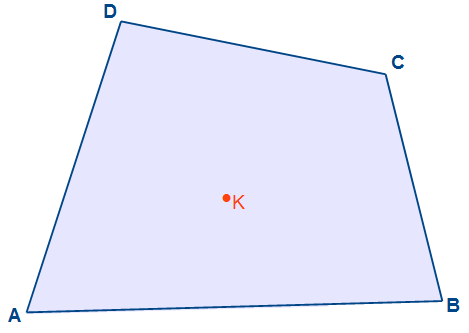
Durch viele viele Schritte gelangt man zeichnerisch zum Kantenschwerpunkt des Vierecks.
