Pyramide
Volumen einer Pyramide
Folgendes Bild zeigt eine Pyramide mit quadratischer Grundfläche:
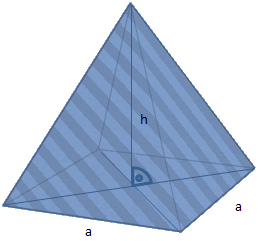
Diese besteht aus einer quadratischen Grundfläche und vier gleichen, dreieckigen Seitenflächen, die oben spitz zusammenlaufen. Die Höhe h steht genau mittig und rechtwinklig auf der Grundfläche.
Das Volumen berechnet sich folgendermaßen:
![]()
Das G in der ersten Formel steht dabei für die Grundfläche der Pyramide welche bei einer quadratischen Pyramide a² ist. Die Formel gilt allerdings auch für alle anderen Pyramiden, welche keine quadratische Grundfläche haben. Wir betrachten hier aber nur quadratische Pyramiden.
Beispiel
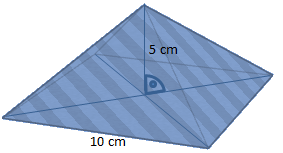
Um das Volumen dieser quadratischen Pyramide zu berechnen, setzen wir die gegebenen Größen einfach in die Formel ein:
![]()
Volumenberechnung wenn h nicht gegeben ist
Nicht immer ist es allerdings der Fall, dass wir die Höhe einer Pyramide gegeben haben. Es kann zum Beispiel sein, dass wir neben der Grundseite a nur die Längen der Außenseiten s gegeben haben:
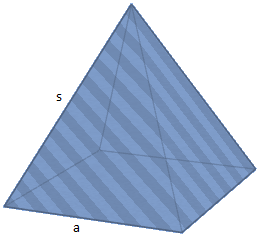
In diesem Fall müssen wir die Höhe zunächst mithilfe von Dreiecken berechnen. Wir können die Höhe mithilfe der folgenden Dreiecke berechnen:
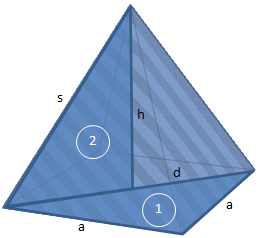
Das Dreieck 1 liegt platt auf der Grundfläche und hilft uns die Diagonale d zu bestimmen. Das Dreieck 2 steht senkrecht auf der Grundfläche. Die Hypotenuse des zweiten Dreiecks ist die Strecke s. Eine Kathete ist genau so lang wie die Hälfte von d, die andere ist die gesuchte Höhe h.
Wir beginnen mit der Berechnung der diagonalen d.
Dreieck 1
Der Pythagoras für Dreieck 1 lautet:
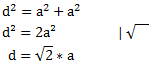
Anschließend können wir mithilfe der Diagonalen und dem Pythagoras für Dreieck 2 die Höhe h berechnen:
Dreieck 2
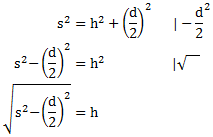
Beispiel
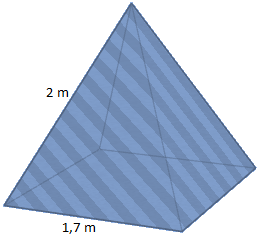
Um das Volumen dieser Pyramide zu berechnen, müssen wir wie eben erklärt vorgehen. Wir berechnen zunächst die Diagonale d mithilfe der Formel
![]()
Anschließend können wir die Höhe h berechnen indem wir d in die eben gezeigte Formel einsetzen:
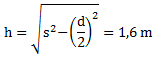
Nun haben wir die Höhe h und können das Volumen berechnen:
![]()
Unser Lernvideo zu : Pyramide
Oberfläche einer Pyramide
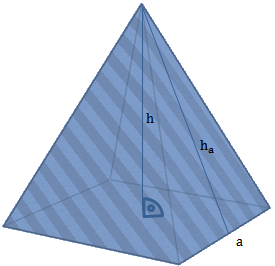
Die Oberfläche einer Pyramide setzt sich zusammen aus der Grundfläche und der Mantelfläche.
![]()
Die Grundfläche berechnet sich bei der quadratischen Pyramide sehr einfach mit der Formel für den Flächeninhalt eines Quadrats:
![]()
Die Mantelfläche setzt sich aus vier kongruenten (gleichen) Dreiecken zusammen. Die Fläche eines dieser Dreiecke berechnet sich mithilfe der Höhe ha:
![]()
Alle vier Dreiecke der Mantelfläche berechnen sich dann folgendermaßen:
![]()
Alternativ kann man auch mit der Höhe h arbeiten. Wir nehmen dafür an, dass die Höhe h und die Grundseite a gegeben sind. Wir müssen ha hierbei zunächst mithilfe des Pythagoras berechnen:
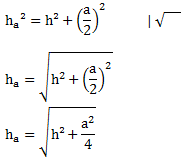
Für die Mantelfläche ergibt sich dann folgendes:
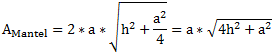
Die Oberfläche kann also mithilfe folgender Formel berechnet werden:
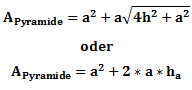
Beispiel
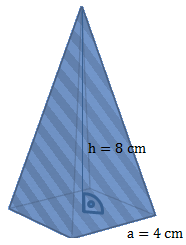
Bei dieser Pyramide ist die Länge der Grundfläche a und die Höhe h gegeben. Wir nutzen für die Oberflächenberechnung die Formel in der diese beiden Größen benötigt werden. Wir rechnen zunächst ohne Einheit. Da alle Angeben in cm sind, müssen wir keine Einheiten umrechnen.
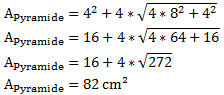
Die Oberfläche der Pyramide beträgt 82 cm².
