Wachstum und Zerfall
Bei einem Vorgang, der entweder einen Wachstum oder einen Zerfall beschreibt, können wir unter zwei Funktionen unterscheiden. Zum einen der Linearen Funktion, auch liniarem Wachstum/Zerfall, und der exponentiellen Funktion, auch exponentiellem Wachstum/Zerfall.
Hier beschreiben wir die beiden Vorgänge und heben ihre Unterschiedeheraus.
Lineares Wachstum/Zerfall
Bei einem Wachstumsvorgang bei dem sich der Funktionswert Schritt für Schritt um denselben Summanden (Wachstumsrate/Zerfallsrate) verändert, sprechen wir von linearem Wachstum oder linearem Zerfall. Die Änderungsrate x ist konstant. Ein solcher Graph ist eine Gerade die bei Wachstum eine positive Steigung hat und bei Zerfall eine negative Steigung darstellt.
![]()
Dieses Thema haben wir bereits auf dieser Homepage berücksichtigt und ihr könnt euch jeder Zeit darüber informieren und euer Wissen auffrischen.
Ein Beispiel für ein lineares Wachstum ist: Ein 1m hohe Planze wächst wöchentlich um 10cm. Die Funktionsgleichung ist hier: f(x) = 0,1x + 1.
Ein Beispiel für einen linearen Zerfall ist: Eine 30cm hohe Kerze brennt pro Stunde 2cm ab. Die Funktionsgleichung ist: f(x) = -2x + 30
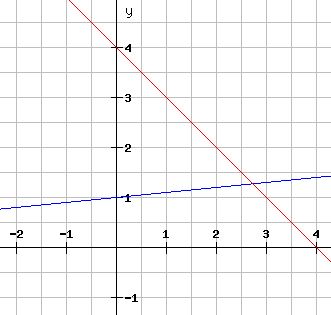
blau: f(x) = 0,1x + 1
rot: f(x) = -2x + 30, bei Graphen verlaufen linear.
Unser Lernvideo zu : Wachstum und Zerfall
Exponentielles Wachstum
Man hat ein exponentielles Wachstum vor sich, wenn der Funktionswert von einem zum nächsten Schritt um denselben Faktor wächst. Sollte es von Schritt zu Schritt um denselben Faktor fallen, sprechen wir von einem exponentiellen Zerfall. Der Graph ist eine Exponentialfunktion. Dazu erfahrt ihr mehr auf der nächsten Seite.
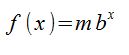
In der Funktionsgleichung seht ihr, dass die Änderungrate im Exponenten steht!
Ein Beispiel für ein exponentielles Wachstum ist: Eine Algenfläche von 3m² erweitert sich monatlich um das dopelte. Die Funktionsgleichung ist: f(x) = 3 • 2x
Ein Beispiel für einen exponentiellen Zerfall ist: Die RAdioaktivität eines Element nimmt pro Jahr um 5% ab. Die Funktionsgleichung ist: f(x) = – 5x
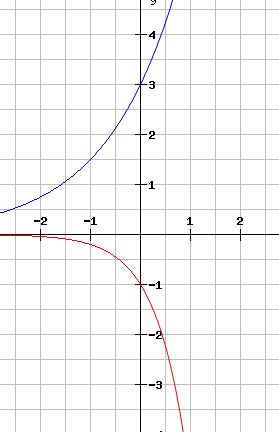
blau: Wachstum
rot: Zerfall
Nun folgt das Thema der exponentiellen Funktionen, die dieses Wachstum und Zerfall noch genauer beschreiben werden.
