Bernoulli Experiment
Was ist der Bernoulli Experiment?
Ein Zufallsexperiment mit genau zwei möglichen Ergebnissen (Treffer oder Niete) nennt man Bernoulli-Experiment.
Formel des Bernoulli-Experiments
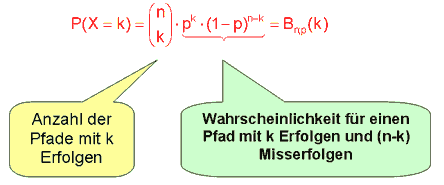
In einer Bernoulli-Kette wird die Wahrscheinlichkeit für einen Treffer bzw. für die 1 als p bezeichnet, wohingegen die Wahrscheinlichkeit eine Niete bzw. 0 als Ergebnis zu erhalten als q bezeichnet wird. Da nur die beiden Zustände vorkommen können, ist die Wahrscheinlichkeit für eine Niete die von 1 (also der Sicherheit) übriggebliebene Wahrscheinlichkeit, einen Treffer zu erhalten. Kurz: q = 1 – p oder p = 1 – q . Die Wahrscheinlichkeit p bzw. q ist eine Zahl zwischen 0 und 1 mit 0 ≤ p ≤ 1 .
Binomialkoeffizient
- Die zu einem n-stufigen Bernoulli-Versuch mit der Erfolgswahrscheinlichkeit p gehörige Verteilung heißt Binomialverteilung mit den Parametern n und p. Die zugehörige Zufallsvariable X heißt binomialverteilt.
- Die Anzahl dieser Pfade kann man mit dem Binomialkoeffizienten (nk) bestimmen. Dieser gibt nämlich an, auf wie viele Arten man die k Erfolge auf die n Stufen der Bernoulli-Kette verteilen kann.
Kann man den Versuch widerholen?
Ja! Man nennt es auch Wiederholte der Bernoulli-Experimente
Wo kommt das Bernoulli Experiment vor?
Einige Aufgaben, bei denen es sich um einen Bernoulli-Prozess handelt:
- Ziehen mit Zurücklegen
- Würfeln
- Glücksrad
- Roulette
Unser Lernvideo zu : Bernoulli Experiment
Beispiel
Ein Würfel wird n=5 mal geworfen. Als Erfolg werten wir die Augenzahl 6. Wie viele Pfade mit k=3 Erfolgen gibt es im Ergebnisbaum?
![]()
Es gibt bei diesem Versuch also insgesamt 10 Pfade, die jeweils 3 Erfolge beinhalten.
Merke Dir
- Ein Bernoulli-Experiment kann als Resultat nur die Ergebnisse 0 oder 1 bzw. Treffer oder Niete besitzen
- Wird ein Bernoulli-Experiment öfter wiederholt, so spricht man von einem Bernoulli-Prozess oder Bernoulli-Kette
- Die Bernoulli-Verteilung ist ein Spezialfall der Binominalverteilung mit n=1.
- Wiederholt man also ein Bernoulli-Experiment öfter und betrachtet alle Ergebnisse, so sind diese binomialverteilt.
- p ist die Wahrscheinlichkeit, dass das Ereignis eintritt;
-
n ist die Anzahl der Versuche (auch Länge der Bernoulli-Kette genannt);
-
k ist die Anzahl der Treffer, die wir erzielen wollen;
-
P(X=k) sagt, dass wir die Wahrscheinlichkeit für genau k Treffer errechnen wollen.
⇒P(X = k) [„genau“],
⇒P(X ≤ k) [„höchstens“] und
⇒P(X ≥ k) [„mindestens“]
