Wahrscheinlichkeitsrechnung Grundlagen
Die Wahrscheinlichkeitsrechnung hilft uns Dinge richtig einzuschätzen und verstehen zu können. Ein klassisches Beispiel ist ein Würfel. Wie Wahrscheinlich ist es, dass eine bestimmte Zahl gewürfelt wird? Diese und andere Fragen möchten wir hier klären.
Unser Lernvideo zu : Wahrscheinlichkeitsrechnung Grundlagen
Grundbegriffe
Wenn man mit einem Würfel würfelt, kann man die Zahlen 1-6 würfeln. Diese Zahlen sind die Ergebnismenge Ω. Jede Zahl die man würfeln kann ist ein Ergebnis das eintreten kann.
Es ist wichtig, dass alle möglichen Ergebnisse in der Ergebnismenge enthalten sind. Man kann jetzt die Wahrscheinlichkeit berechnen, dass ein bestimmtes Ereignis eintritt. Das Ereignis E ist also eine Menge, in der wir formulieren, von was wir die Wahrscheinlichkeit ausrechnen möchten.
Das Gegenereignis enthält dagegen alle Ergebnisse die nicht in der Ereignismenge enthalten sind. Die Wahrscheinlichkeit P ist nun der Prozentsatz zu dem ein Ergebnis aus der Ereignismenge eintritt.
Die Gegenwahrscheinlichkeit ist die Wahrscheinlichkeit zu der ein anderes Ergebnis eintritt.
Beispiel:Wurf mit einem Würfel (6 Flächen)
Ein Würfel hat genau sechs mögliche Ergebnisse. Die Ergebnismenge ist also:
Ω = {1, 2, 3, 4, 5, 6}
Wir möchten nun ausrechnen wie wahrscheinlich es ist, dass wir eine Zahl kleiner als 4 würfeln. Das Ereignis enthält damit alle Zahlen kleiner als 4:
E = {1, 2, 3}
Das Gegenereignis ist damit:
![]()
Ein Würfel ist nun typischerweise so gebaut, dass der Wurf jeder Zahl gleichwahrscheinlich ist. Es ist also genauso wahrscheinlich eine 1 zu würfeln wie eine 6 zu würfeln. Da wir beim Würfel 6 Seiten haben können wir für die Wahrscheinlichkeit P schreiben:

Wenn wir nun die Wahrscheinlichkeit bestimmen wollen mit der eine Zahl kleiner als 4 gewürfelt wird, müssen wir einfach die Wahrscheinlichkeiten der einzelnen Ergebnisse addieren die im Ereigniserhalten sind
![]()
Die Wahrscheinlichkeit, dass eine Zahl kleiner als 4 gewürfelt wird beträgt somit 50%.
Ergebnisse gleicher Wahrscheinlichkeit
Immer wenn alle Ergebnisse gleich wahrscheinlich sind, kann man die Wahrscheinlichkeit auch folgendermaßen berechnen:
![]()
Bei einem Würfel also:
![]()
Bestimmen einer unbekannten Wahrscheinlichkeit durch probieren
Bei einem Würfel ist es relativ einfach die Wahrscheinlichkeit zu ermitteln. Was ist aber mit einem Würfel bei dem eine Kante länger ist als die anderen? Hier wird es schwer die Wahrscheinlichkeit zu berechnen. Oder was passiert bei einer Münze die verbogen ist?
Auch hier wird es schwierig. Wir können die Wahrscheinlichkeit in so einer Situation mit einem Experiment bestimmen. Wir werfen eine verbogene Münze sehr oft (zum Beispiel 100-mal) und notieren uns immer wie rum sie gelandet ist. Wenn wir dies sehr oft machen, bekommen wir vielleicht folgendes Ergebnis:
Zahl = 41
Kopf = 59
Um diese absoluten Werte in Wahrscheinlichkeiten umzurechnen teilen wir die Zahlen durch die Anzahl der Würfe:
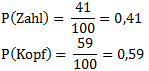
Wir sehen also das die Wahrscheinlichkeit bei dieser Münze Zahl zu erhalten 41% ist. Dies ist natürlich noch kein sehr genauer Wert, da wir nur 100-mal geworfen haben. Einen besseren Wert erhalten wir wenn wir wenn wir öfter werfen. Wir werfen deshalb 1000-mal:
Zahl = 395
Kopf = 605
Wir teilen wieder durch die Anzahl:
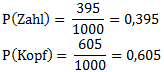
Wir sehen also nun relativ gut, dass diese Münze sich nicht wie eine normale Münze verhält bei der beide Ergebnisse zu je 50% eintreten sollten. Bei unserer Münze hingegen bekommen wir deutlich öfter das Ergebnis Kopf.
