Würfel Wahrscheinlichkeit
Wir alle kennen den klassischen Würfel. Er hat sechs Seiten. Diese Seiten sind nummeriert von 1 bis 6. Gerne wird der Würfel in der Wahrscheinlichkeitsrechnung genutzt, weil er jedem bekannt ist. Solange der Würfel nicht manipuliert ist oder anders unausgeglichen ist, ist die Wahrscheinlichkeit eine 1 zu werfen genauso hoch wie eine 6 zu werfen. Diese Wahrscheinlichkeit schauen wir uns nun genau an.
Baumdiagramm Würfel
Oft wird ein Baumdiagramm genutzt um Würfelwürfe darzustellen. Die Wahrscheinlichkeit bei einem Würfel wird wie folgt berechnet: Wir zählen die möglichen Ergebnisse. In dem Fall des Würfels sind es sechs Möglichkeiten. Diese Zahl wird in einem Bruch in den Nenner geschrieben:
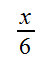
Bei einem Wurf eines Würfels kann genau eine Zahl gewürfelt werden. Dies setzten wir in den Nenner:
![]()
Dies bedeutet, dass wir bei jedem Wurf eines Würfels eine Wahrscheinlichkeit von einem sechstel haben eine bestimmte Zahl zu werfen. Egal welche Zahl wir werfen, es ist immer die selbe Wahrscheinlichkeit.
Im Baumdiagramm dargestellt sieht es wie folgt aus:
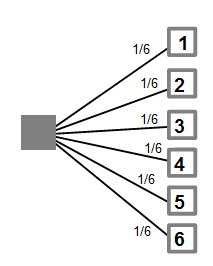
In der Abbildung sehen wir ein Baumdiagramm, was von einem Punkt aus geht. Wir haben sechs mögliche Ergebnisse, die alle gleichwertig sind. Daher ist die Wahrscheinlichkeit bei einem Wurf eine 5 zu werfen einsechstel groß. Jede andere Zahl hat den selben Wert.
Beispiele
1) Bei einem Wurf eine 3 zu werfen. Die Wahrscheinlichkeit ist: 1/6.
2) Bei einem Wurf eine 4 zu werfen. Die Wahrscheinlichkeit ist: 1/6.
3) Bei einem Wurf eine gerade Zahl zu werfen. Auf einem Würfel haben wir 3 gerade Zahlen: 2, 4 und 6. Nun haben wir drei gewünschte Ergebnisse und 6 Ausgangsmöglichkeiten. Das bedeutet die Wahrscheinlichkeit lieg bei 3/6 = 1/2.
4) Bei einem Wurf eine 1 oder 2 zu werfen. Nun haben wir zwei gewünsche Ergebnisse und 6 Ausgangsmöglichkeiten. Das bedeutet, dass die Wahrscheinlichkeit hierfür bei 2/6 = 1/3 liegt.
Mehrmaliges Werfen
Werfen wir den einen Würfel nun nicht nur einmal, sondern zwei oder mehrmals, müssen wir jeden Wurf einzeln betrachten. Somit ist die Wahrscheinlichkeit bei jedem Wurf wieder 1/6. Im Baumdiagramm kann man dies wie folgt darstellen:
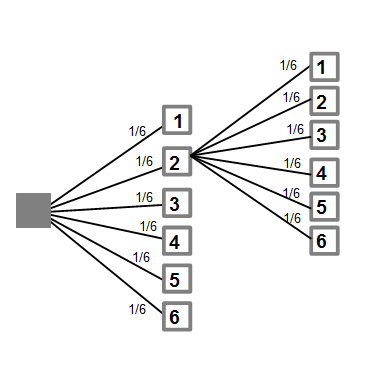
In dieser Abbildung sehen wir, wie ein Würfel zweimal geworfen wird. Um den Überblick zu behalten gehen wir davon aus, dass beim ersten Wurf eine 2 gewurfen wurde. Die Wahrscheinlichkeit dabei war 1/6. Nun wird ein zweites Mal geworfen und wieder ist fü jede Zahl auf dem Würfen die Wahrscheinlichkeit zu erscheinen 1/6.
Beispiele:
1) Zunächst eine 2 und dann eine 3 werfen. Die Wahrscheinlichkeit für eine 2 lag bei 1/6. Beim zweiten Wurf eine drei zu werfen liegt auch bei 1/6. Für die Kombination aus erst 2 und dann 3 zu werfen liegt dann bei
1/6 • 1/6 = 1/36. Die einzelnen Wahrscheinlichkeiten werden multipliziert. In Prozent aus gedrückt wären das 1/36 • 100 = 2,78%.
2) Zunächst eine 2 und dann eine weitere gerade Zahl zu werfen. Beim ersten Wurf ist die Wahrscheinlichkeit 1/6. Beim zweitn Wurf liegt sie bei 3/6 = 1/2. Diese beiden Wahrscheinlichkeiten werden multipliziert: 1/6 • 1/2 = 1/12. In Prozent sind das 1/12 • 100 = 8,3%.
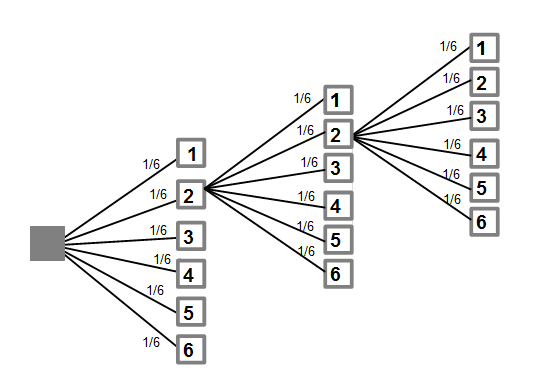
Diese Abbildung zeigt einen dreifachen Wurf. Natürlich kann man das Diagramm bis ins unendliche fortführen und die verschiedenen Möglichkeiten von Ergebnissen berechnen.
Des weiteren besteht nun auch die Möglichkeit, dass mit mehreren Würfeln geworfen wird. Trotz mehrere Würfel ist jeder einzelne Würfel zu berechnen. Das heißt bei jedem Würfel ist bei jedem Wurf die Wahrscheinlichkeit für eine bestimmte Zahl immer 1/6.
Beispiele:
1) Mit zwei Würfeln einen Pasch beim einmaligen werfen zu würfeln. Jeder Würfel hat eine Wahrscheinlichkeit von 1/6. 1/6 • 1/6 = 1/36. Da es 6 mögliche Paschs gibt ist die Wahrscheinlichkeit 6/36 =1/6. Somit liegt die Wahrscheinlichkeit einen beliebigen Pasch mit zwei Würfeln zu werfen bei 16,67%.
2) MIt fünf Würfeln einen „Kniffel“ zu werfen. Also mit einem Wurf haben alle fünf Würfel die selbe Zahl. Jeder Würfel hat die Wahrscheinlichkeit von 1/6. Fün Würfel somit die Wahrscheinlichkeit von 1/7776. Es gibt 6 verschiedene Möglichkeiten: 6/7776 = 1/1296. Das entspricht 0,08% Wahrscheinlichkeit.
Interessante Fragen und Antworten zu Würfel Wahrscheinlichkeit
Wie macht man ein Baumdiagramm? |
| Am Anfang eines Baumdiagrammes stehen mehrere Punkte. Der Würfel ist ein guter Partner um dieses Diagramm erstellen zu können. Auf dem Würfel befinden sich die Punkte von eins bis sechs. Nun wird anhand des Baumdiagrammes eine Wahrscheinlichkeitsberechnung durchgeführt.Wer einen Würfel wirft, kann in der Regel nicht sagen, welche Zahl angezeigt wird. Daher ist die Wahrscheinlichkeit zunächst auch bei einer Quote von 1/6. Es könnte eine Zahl auf dem Würfel angezeigt werden von den 6 vorhandenen. Zunächst ist jedoch der Ausgangspunkt für das Baumdiagramm überaus wichtig. Die Wahrscheinlichkeitsberechnung gehört heute zum Schulwissen einfach dazu und jeder sollte sie sich auch zu Herzen nehmen.
Nur wer Berechnungen wirklich ernst nimmt, kann dann auch zu einem guten Ergebnis gelangen. Das Baumdiagramm schließt sich nach hinten und auf dem Weg dorthin werden die Quoten berechnet. Wie hoch ist also die Chance eine 4 auf dem Würfel oben liegen zu haben. Vieles ist für die Nutzer einfacher, wenn sie sich lange genug damit beschäftigen. Auch ein Baumdiagramm lässt sich mathematisch sicher gut erklären. Dennoch sollte der Nutzer auch wissen, wofür es gut ist. Das Baumdiagramm wird mit Hilfe von bestimmten Werkzeugen gezeichnet. Es kann auch von Hand gezeichnet werden, aber dann ist es leider nicht so akkurat und wird auch nicht in einer Arbeit darüber abgenommen. Der Nutzer sollte nun auf jeden Fall sicher sein, dass er alles beachtet hat, um das Diagramm so sauber wie möglich zu bekommen. Wer nun auf Nummer sicher geht, wird schon bald erfolgreicher damit sein und kann stolz sein. |
