Wurzelgleichungen
Eine Wurzelgleichung ist eine Gleichung, in der die Variable unter einer Wurzel steht. Zum Lösen einer Wurzelgleichung nutzt man die Äquivalenzumformung von Gleichungen, die wir bereits bei dem Thema „Lineare Gleichung“ besprochen haben. Gerne könnt ihr euch dieses noch mal anschauen. Dazu gekommen sind nun die Wurzeln, die man auflösen muss, um zum Ergebnis zu gelangen.
Zur Erinnerung
Unter einer Wurzel verstehen wir die das Radizieren (Wurzelziehen) einer Potenz. Also ist die Wurzel die Umkehrfunktion einer Potenz. Somit hebt die Quadratwurzel die Potenz 2. Grades auf, die 3. Wurzel die Potenz 3. Grades usw.
Dies nehmen wir uns beim Lösen von Wurzelgleichungen zu Nutze.
Unser Lernvideo zu : Wurzelgleichungen
Lösen von Wurzelgleichungen
Das Lösen von Wurzelgleichungen kann man in 5 Schritten beschreiben, die allgemein anwendbar sind.
1. Schritt: Die Wurzel wird isoliert. Dabei wird die Gleichung durch Äquivalenzumformungen so geändert, dass die Wurzel allein auf einer Seite der Gleichung steht.
2. Schritt: Die Wurzel wird aufgehoben. Dabei wird nachgeschaut, um welche Wurzel es sich handelt, ob es eine Quadratwurzel ist, eine Wurzel 3. Grades usw. Bei einer Wurzel 2. Grades wird die Gleichung quadiert, um die Wurzel aufzulösen, bei einer Wurzel 3. Grades wird die Gleichung mit der Potenz 3 berechnet etc.
3. Schritt: Die Gleichung wird nun mit Äquivalenzumformungen nach der gesuchten Variablen aufgelöst.
4. Schritt: Die Lösung wird durch eine Probe überprüft, in dem man sie ind ie Ausgangsgleichung setzt.
5. Schritt: Die Lösungsmeinge wird angegeben.
Mit diesen 5 Schritten könnt ihr eine Wurzelgleichung lösen. Wichtig ist natürlich zu beachten, dass bei einer Äquivalenzumformung immer auf beiden Seiten die Rechnung durchgeführt werden muss. Wir betrachten ein paar Beispiele um uns die Schritte nochmal zu vergegenwärtigen.
Beispiel 1
Berechnen der folgenden Gleichung:
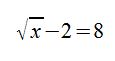
Wir gehen dabei die einzelnen Schritte Durch. Isolieren zunächst die Wurzel, dann wird die Gleichung quadriert, dann nach x aufgelöst und ausgerechnet.
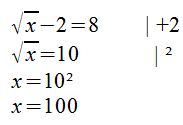
Im ersten Schritt haben wir + 2 gerechnet, um die Wurzel zu isolieren, danach wurde quadriert, da wir hier eine Quadratwurzel haben. Da wir dann direkt nach der Variablen auch aufgelöst haben, können wir das Ergebnis berechnen. Die Lösungsmenge L ist hier 100. Die Probe:
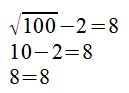
Somit haben wir die Aufgabe richtig gelöst. L={100}
Beispiel 2
![]()
Auch bei dieser Gleichung gehen wir Schritt für Schritt vor, so dass wir am Ende nach x aufgelöst haben.
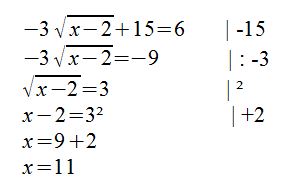
Zunächst wird die Wurzel isoliert, danach können wir die Gleichung quadrieren. So haben wir dann noch x-2 = 9. Danach lösen wir nach x auf und erhalten unsere Lösung x= 11. Wir nutzen die Probe:
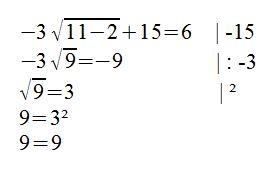
Die Aufgabe ist richtig gelöst. L ={11}
Beispiel 3
![]()
Bei dieser Gleichung haben wir nun auf jeder Seite eine Wurzel. Dennoch bearbeiten wir auch diese Gleichung mit den selben Schritten wie die vorherigen Beispiele.
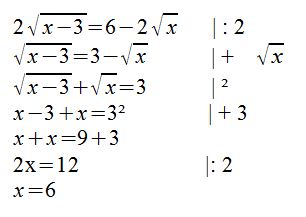
Wir haben zunächst wieder die Wurzeln isoliert und auf eine Seite gebracht, mit dem Quadrieren wurden die Wurzeln entfernt und wir können nach x auflösen. Die Probe wird zeigen, ob wir richtig gerechnet haben:
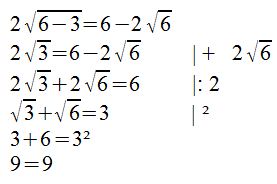
Auch hier haben wir die richtige Lösung ermittelt, somit ist L = {6}
Nun seid ihr gewappnet für diese und ähnliche Aufgaben. Wichtig ist, sich nicht aus der Ruhe bringen zu lassen und einen Schritt nach dem nächsten zu machen.
