y-Achsenabschnitt berechnen
y-Achsenabschnitt berechnen: Wie man in verschiedenen Situationen den y-Achsenabschnitt bestimmen und berechnen kann erklären wir hier.
Unser Lernvideo zu : y-Achsenabschnitt berechnen</h2
y-Achsenabschnitt bestimmen
Wenn man die Funktionsvorschrift hat, ist die Bestimmung des y-Achsenabschnitts b natürlich sehr leicht, da dieser direkt in der Funktion steht.
Beispiele y-Achsenabschnitt bestimmen
f(x) = 3 • x + 5 y-Achsenabschnitt b = 5
g(x) = 3 • x – 2 y-Achsenabschnitt b = -2
h(x) = 3 • x + 7 y-Achsenabschnitt b = 7
i(x) = 3 • x y-Achsenabschnitt b = 0
Wenn wir dagegen einen Graphen haben müssen wir den y-Achsenabschnitt vom Graphen ablesen. Dieser ist dabei immer der Schnittpunkt mit der y-Achse:
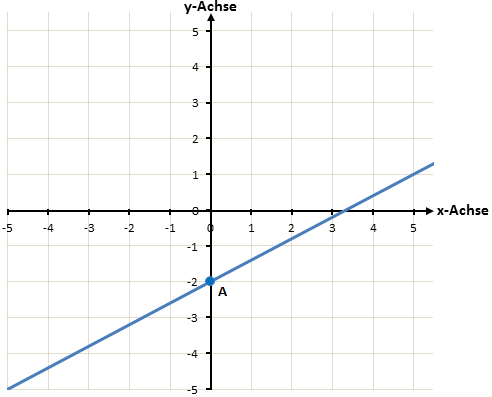
Der Punkt A muss also abgelesen werden. In diesem Beispiel ist der Punkt A(0/-2). Der y-Achsenabschnitt ist also gleich b = -2 (Immer die y-Koordinate des Schnittpunkts).
Den y-Achsenabschnitt berechnen hilft, die Gleichung einer Funktion aus ihrem Graphen heraus zu erstellen.
Der y-Achsenabschnitt ist Teil der Funktionsgleichung
Der y-Achsenabschnitt einer linearen Funktion ist der Abstand des Schnittpunktes von x- und y-Achse (Nullpunkt) und dem Schnittpunkt des Graphen mit der y-Achse. Er ist ein wesentlicher Bestandteil der Gleichung einer Funktion. Die Standardgleichung einer linearen Funktion ist:
y = mx + b
Das b bezeichnet den y-Achsenabschnitt, m die Steigung des Graphen.
Beispiel eines abzulesenden y-Achsenabschnittes
In diesem Teil geht es um den y-Achsenabschnitt einer linearen Funktion. Diese ist immer als Gerade im Koordinatensystem darstellbar. Seine Achsen sind mit x und y bezeichnet. Die x-Achse verläuft von links nach rechts, die y-Achse von oben nach unten. Im Koordinatensystem befindet sich der Graph. Falls er die y-Achse in einem gut abzulesenden Punkt schneidet, ist keine Berechnung notwendig. Die Zahl ist ablesbar und in die Gleichung einsetzbar. Jeden y-Achsenabschnitt berechnen wir mit dem x-Wert 0, da auf der Höhe der y-Achse jeder ihrer Punkte für im x-Wert 0 beträgt.
Im folgenden Beispiel schneidet der Funktionsgraph die y-Achse im Punkt (0/-1). Als Bezeichnung des y-Achsenabschnittes dient der y-Wert, der bei jedem Graphen einen anderen Wert annimmt. In diesem Fall beträgt er (-1). Die Gleichung der Beispielsfunktion lautet:
(-1) = m * 0 + (-1)
Da laut Definition
m * 0 = 0
ist der Term aus der Gleichung zu entfernen. Es bleibt:
(-1) = (-1)
In jedem Koordinatensystem wo der Graph die y-Achse in einem gut einsehbaren Punkt schneidet, ist der ablesbare Wert auf der y-Achse gleich dem y-Achsenabschnitt. Berechnen ist notwendig, falls der Schnittpunkt sich außerhalb des sichtbaren Koordinatensystems befindet oder falls der Wert viele Kommastellen aufweist.
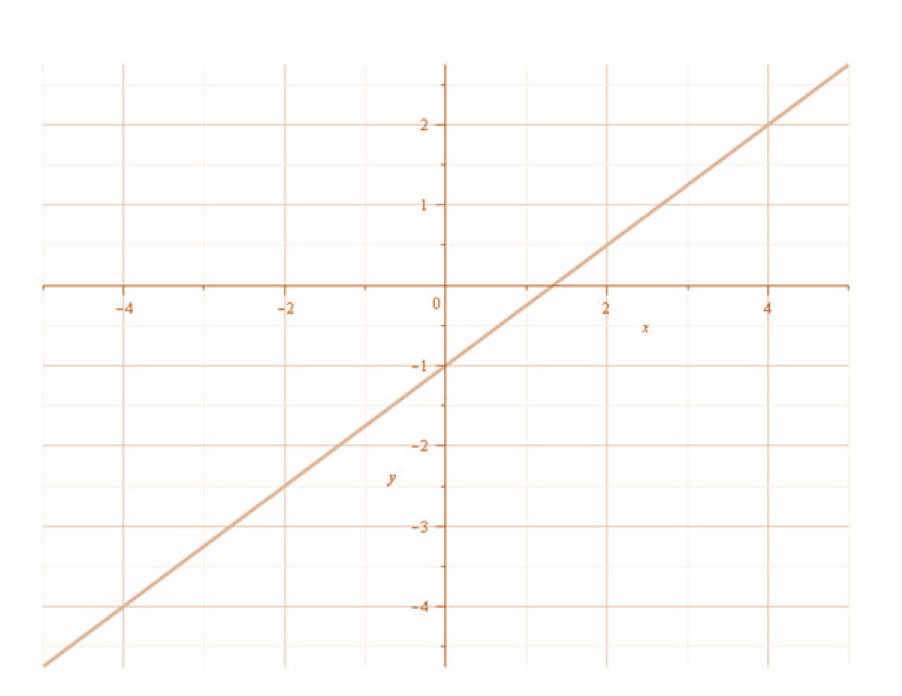
Den y-Achsenabschnitt berechnen
Die Berechnung im selben Beispiel ist einfach zu zeigen. Für die Elaboration der Funktionsgleichung nehme ich einen gut sichtbaren Punkt. Dies ist in dem Fall der Punkt (0/-1). Ich setze das entsprechende x und das y in die Standardgleichung ein:
(-1) = m * 0 +b.
Laut den Multiplikationsregeln ist m*0 = 0. Die Gleichung lautet: (-1) = 0 +b. Das bedeutet der Term ist aus der Gleichung eliminierbar. Es bleibt (-1) = b. Somit ist bewiesen, dass der y-Achsenabschnitt (-1) beträgt und mit dem Abstand zwischen dem 0-Punkt und dem Schnittpunkt des Graphen mit der y-Achse identisch ist.
Der Graph einer linearen Funktion ist eine Gerade. Somit ist klar, dass die Steigung der Geraden in jedem Punkt des Graphens gleich ist. Die Berechnung des Steigungsdreieckes ist nur notwendig, falls sich der Schnittpunkt nicht auf dem sichtbaren Teil des Koordinatensystems befindet. Den y-Achsenabschnitt berechnen reicht, um die Gleichung aus einem gegebenen Graphen abzulesen.
Berechnung der Steigung m eines Graphen
In der Standardgleichung
y = mx + b
bezeichnet das m die Steigung. Ihre Berechnung im folgenden Beispiel funktioniert so:
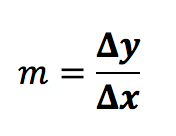
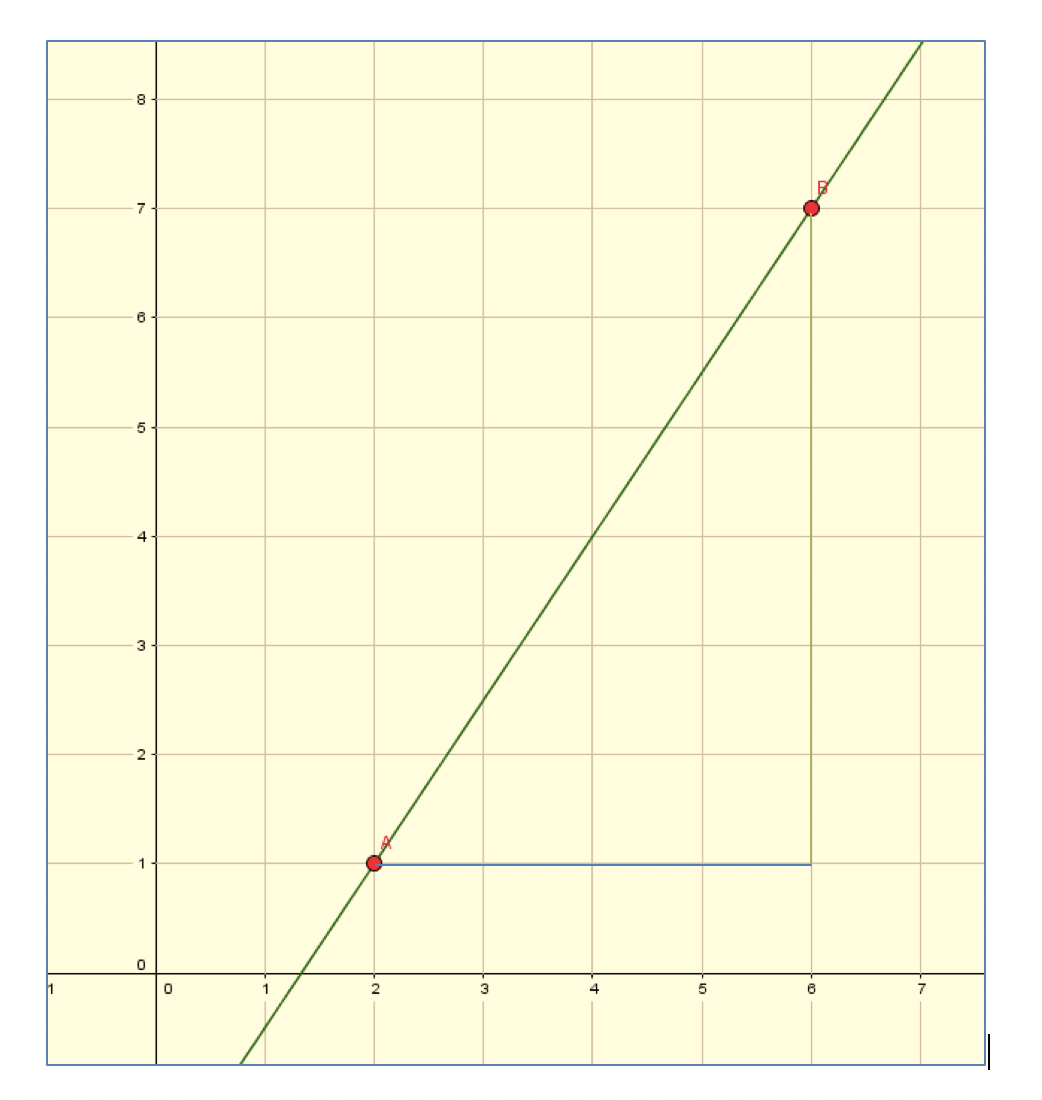
Delta y bedeutet die Länge der Kathete BC in Einheiten. Delta x ist die Länge der Kathete AC. Das Steigungsdreieck befindet im untenstehenden Graphen zwischen Punkt A (2/1) und Punkt B (6/7) auf dem Graphen.
Die Hypotenuse des Dreiecks befindet sich auf dem Funktionsgraphen. Zusammen mit der Linie von A parallel zur x-Achse und der von B aus parallel zur y-Achse bildet sie ein Dreieck. Punkt C ist der Schnittpunkt der von A und der von B ausgehenden Linien. Er hat die Koordinaten (6/1). Die Gleichung lautet:
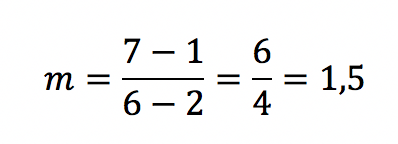
Die Steigung m beträgt 1,5.
Im obenstehenden Graphen ist der y-Achsenabschnitt nicht zu sehen. Die Berechnung ist notwendig, um ihn zu bestimmen. Den y-Achsenabschnitt berechnen geschieht mithilfe der Steigung. In der Standardgleichung ist m einzusetzen:
y = 1,5 x + b
Mit den Koordinaten eines beliebigen Punktes ist b zu berechnen.
Der Einfachheit halber ist der gewählte Punkt A mit den Koordinaten (2/1). Die Gleichung lautet:
1 = 1,5 * 2 +b
Der nächste Schritt ist die Auflösung der Gleichung nach b.
1= 1,5 * 2 + b -> multiplizieren
1 = 3 + b -> -3
-2 = b
Der y-Achsenabschnitt ist -2. Das bedeutet: Der Graph schneidet die y-Achse im Punkt (0/-2).
Den y-Achsenabschnitt berechnen aus Gleichungen
Bis jetzt war der Ausgangspunkt die Grafik. Wie ist der y-Achsenabschnitt zu berechnen, wenn nur die Funktionsgleichung vorhanden ist? Der Maßstab ist die Standardgleichung:
y = mx + b
Die folgenden Beispiele sind gleich aufgebaut.
y = 4x + 3
In dieser Funktionsgleichung beträgt der y-Achsenabschnitt:
b = +3
y = 4x -2
Den y-Achsenabschnitt berechnen bei dieser Gleichung ist überflüssig. Das Ergebnis
b = (-2)
ist einfach abzulesen.
y = 4x
Bei dieser Funktionsgleichung fehlt der Teil mit dem y-Achsenabschnitt. Er beträgt:
b = o
Der Graph geht somit durch den Punkt (0/0), den Nullpunkt des Koordinatensystems.
Was bedeutet Steigung?
Beim Thema Funktion ist dem Begriff Steigung eine wichtige Rolle zuzuordnen. Sie ist definiert als Maß der Steilheit einer Geraden oder Kurve. Die Steigung einer Geraden ist zu berechnen. Sie ist mit dem Buchstaben m bezeichnet. Ihre Formel lautet:
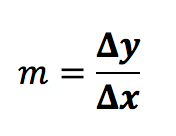
Ihre Berechnung geschieht bei geraden Graphen und anderen Funktionen.
x-Achse und y-Achse
Die beiden Achsen bilden das Koordinatensystem. Sie stehen im rechten Winkel zueinander. Die x-Achse liegt waagrecht, während die y-Achse senkrecht durch den 0-Punkt der x-Achse verläuft. Der Schnittpunkt der beiden Achsen ist der 0-Punkt des Koordinatensystems. Die Abschnitte auf den Achsen sind mit ganzen Zahlen bezeichnet. Der 0-Punkt hat nicht obligatorisch sichtbar zu sein, falls der Graph in einem anderen Abschnitt zu prüfen ist.
Punkte im Koordinatensystem
Den y-Achsenabschnitt berechnen mithilfe des Graphen funktioniert gut. Jeder Punkt ist durch zwei Ziffern genau definiert. Ein Punkt hat die Form (x/y). Sie definiert ihn durch die Lage zwischen den beiden Achsen. Die Reihenfolge ist einzuhalten. Die Lage in Zusammenhang mit der x-Achse ist die erste Ziffer. Die zweite bezieht sich auf seine Lage relativ zur y-Achse.
Zum y-Achsenabschnitt berechnen braucht es den Schnittpunkt des Graphen mit der y-Achse. Falls dieser nicht ablesbar ist, dienen zwei beliebige Punkte auf dem Graphen dazu, die Steigung m zu erhalten. Beide Wege führen zum selben Ergebnis. Falls nur die Funktionsgleichungen vorhanden sind, ist die Berechnung auf rein mathematischem Wege die Lösung.
