Zeichnen einer quadratischen Funktion
Wenn man die Funktionsvorschrift hat, ist es relativ einfach eine Funktion zu zeichnen. Das Vorgehen ist dabei dasselbe wie auch bei den linearen Funktionen. Zunächst einmal müssen wir eine Wertetabelle anlegen mit dem für uns relevanten Bereich. Anschließend können wir die Punkte in ein geeignetes Koordinatensystem eintragen.
Beispiel Normalparabel
Die Normalparabel hat eine sehr einfache Funktionsvorschrift:
f(x) = x²
Wir legen zunächst eine Wertetabelle an. Hier müssen wir uns entscheiden welche x-Werte wir vorgeben möchten. Wenn man noch nicht weiß wie eine Funktion aussehen wird, ist es oft sinnvoll einige negative und einige positive Werte zu berechnen. Wenn man schon weiß wo der Scheitelpunkt (was das ist wird später erklärt) liegt, kann man sich am besten danach richten.
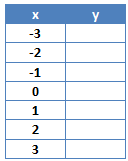
Jetzt können wir zu jedem x-Wert den dazugehörigen y-Wert berechnen indem wir den x-Wert in die Funktionsvorschrift einsetzen. Dabei müssen wir darauf achten, dass wir negative Zahlen in Klammern setzen müssen. Für die -3 müssen wir also rechnen:
f(-3) = (-3)² = 9
Dadurch ergibt sich folgende Wertetabelle:
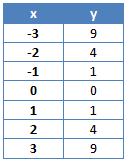
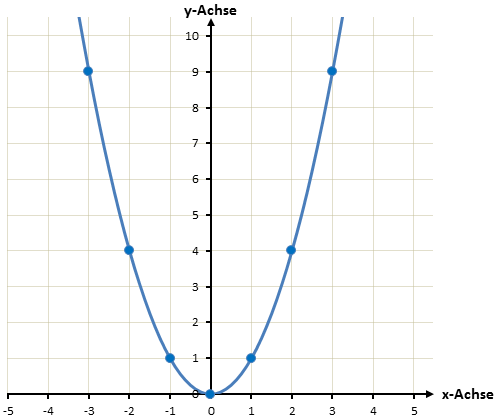
Diese Punkte können wir nun in das Koordinatensystem einzeichnen:
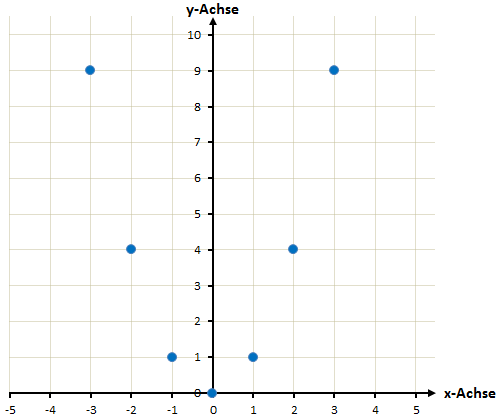
Jetzt verbinden wir die Punkte. Dabei dürfen wir kein Lineal verwenden, sondern sollten versuchen eine durchgehende Linie zu zeichnen die keine Knicke hat.
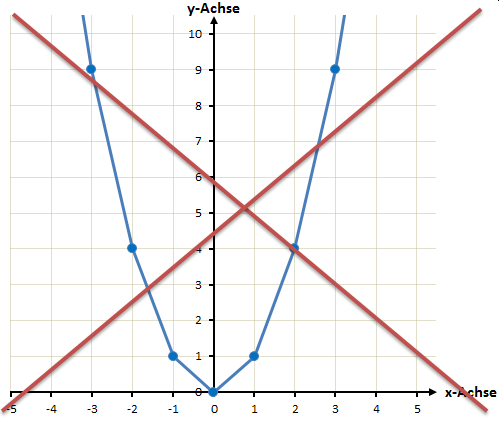
Beispiel 2
f(x) = 0,2x² – x – 4
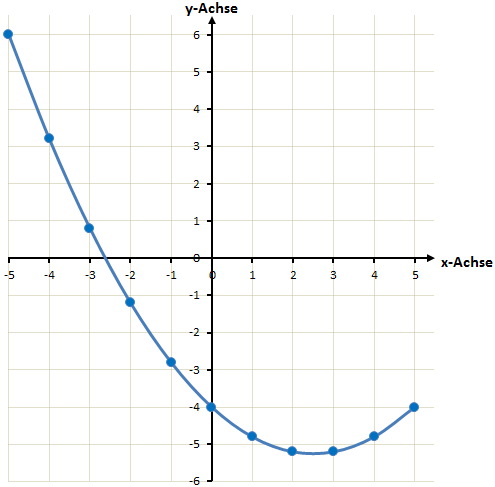
Um diese Funktion zu zeichnen erstellen wir genau wie eben eine Wertetabelle. Da wir den Scheitelpunkt nicht kennen legen wir diese etwas breiter an und berechnen die Funktionswerte von x=-5 bis x=5.
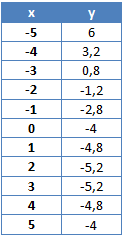
Wir müssen uns die y-Werte nun angucken um unser Koordinatensystem richtig zu zeichnen. Auf der x-Achse muss es von -5 bis 5 gehen. Auf der y-Achse haben wir Werte zwischen -5,2 und 6. Wir legen die y-Achse also von -6 bis +6 an und zeichnen die Werte ein.