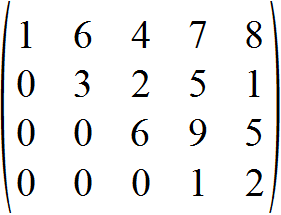Zeilenstufenform
Die Zeilenstufenform wird auch einfach Stufenform oder Treppenform genannt und ist eine von vielen Formen, die Matrizen annehmen können. Im Grunde kann jede Matrix in die Zeilenstufenform gebracht werden. Eine vereinfachte Definition lautet:
- Von oben nach unten gesehen müssen in jeder Zeile der Matrix am Anfang mehr Nullen stehen als in der vorherigen Zeile.
Hierdurch entstehen die namensgebenden Stufen, die auch im folgenden Beispiel zu sehen sind:
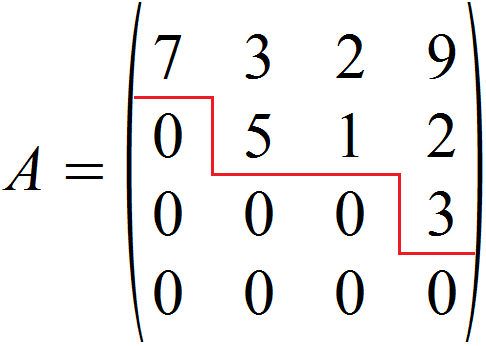

Eine Matrix kann über verschiedene Zeilenstufenformen verfügen, oftmals gibt es also mehrere Lösungen. Die Anzahl der Nullzeilen ist in jeder Zeilenstufenform einer Matrix jedoch gleich!
Die Dreiecksform ist eine spezielle Form der Zeilenstufenform.
Umformung anhand eines Beispiels
Um eine beliebige Matrix in die Zeilenstufenform zu bringen, bedient man sich des Gauß-Algoritmus. Hierbei darf man:
- Zeilen addieren oder subtrahieren
- Zeilen mit einer Zahl multiplizieren oder durch eine Zahl dividieren
- Zeilen vertauschen
Aufgabe
Folgende Matrix A soll in die Zeilenstufenform gebracht werden.
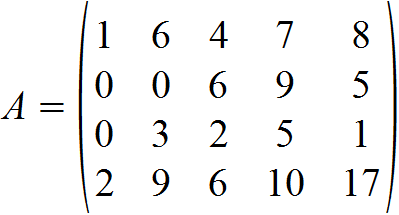
Mit Blick auf die rot markierte 2 ziehen wir die erste Zeile zweimal von der vierten Zeile ab, um an der besagten Stelle eine Null zu erhalten.
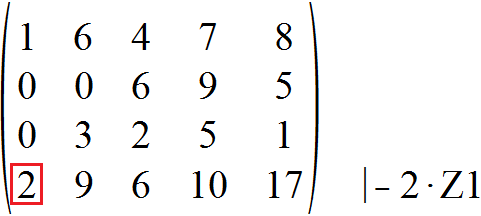
Betrachten wir nun die vier Elemente im roten Quadrat. Es bieten sich an, hier eine der beiden Zeilen zu der anderen zu addieren, um zwei weitere Elemente gleich Null zu erhalten. Wir addieren also die dritte Zeile zur vierten Zeile.
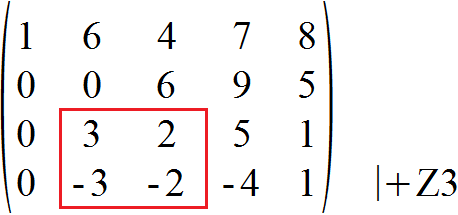
Laut der Definition für die Zeilenstufenform müssen von oben nach unten gesehen in jeder Zeile am Anfang mehr Nullen stehen als in der jeweils vorherigen. Wie wir anhand der vier Elemente im roten Quadrat sehen, bietet es sich hier an, die zweite und dritte Zeile zu tauschen.
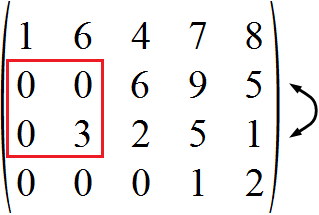
Geschafft! Uns liegt nun die gewünschte Zeilenstufenform vor, wie anhand der roten Treppe zu erkennen ist. In jeder Zeile befinden sich vorne mehr Nullen als in der jeweiligen Zeile zuvor.
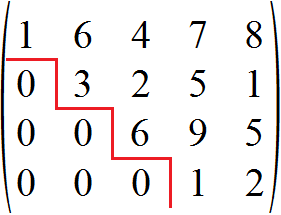
Wir erhalten also folgende Matrix als eine Zeilenstufenform von A: